Предмет: Алгебра,
автор: Аноним
''''''''''''''''''''
Приложения:
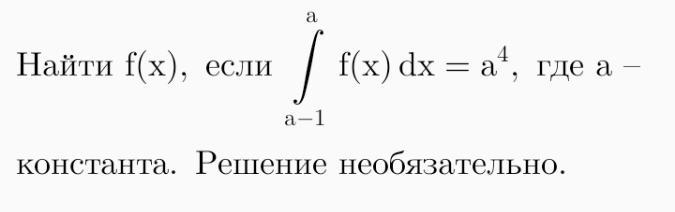
azargun:
я незнаю
ребят помогите ему страдает уже 6 часов
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Будем считать, что подынтегральная функция интегрируема по Риману на отрезке
.
Тогда, воспользовавшись дифференцированием по параметру , получим:
- линейное неоднородное рекуррентное соотношение.
Характеристическое уравнение .
Частное решение ищем в виде .
Подставляя в рекуррентное соотношение и рассматривая точки , получим систему для коэффициентов:
Из первых двух уравнений, сложив их, получим . Тогда, с учетом третьего,
. Значит,
и
, откуда
.
Итак, решением системы является .
Значит, .
Подставив полученную функцию в условие, найдем значение константы :
Полученная функция удовлетворяет условию.
Только кроме интегрируемости ещё непрерывность добавить нужно.
Похожие вопросы
Предмет: Русский язык,
автор: Кatrin13
Предмет: Қазақ тiлi,
автор: тёмный3
Предмет: Русский язык,
автор: МарселинАбадир123
Предмет: Математика,
автор: vitysik3454