Question

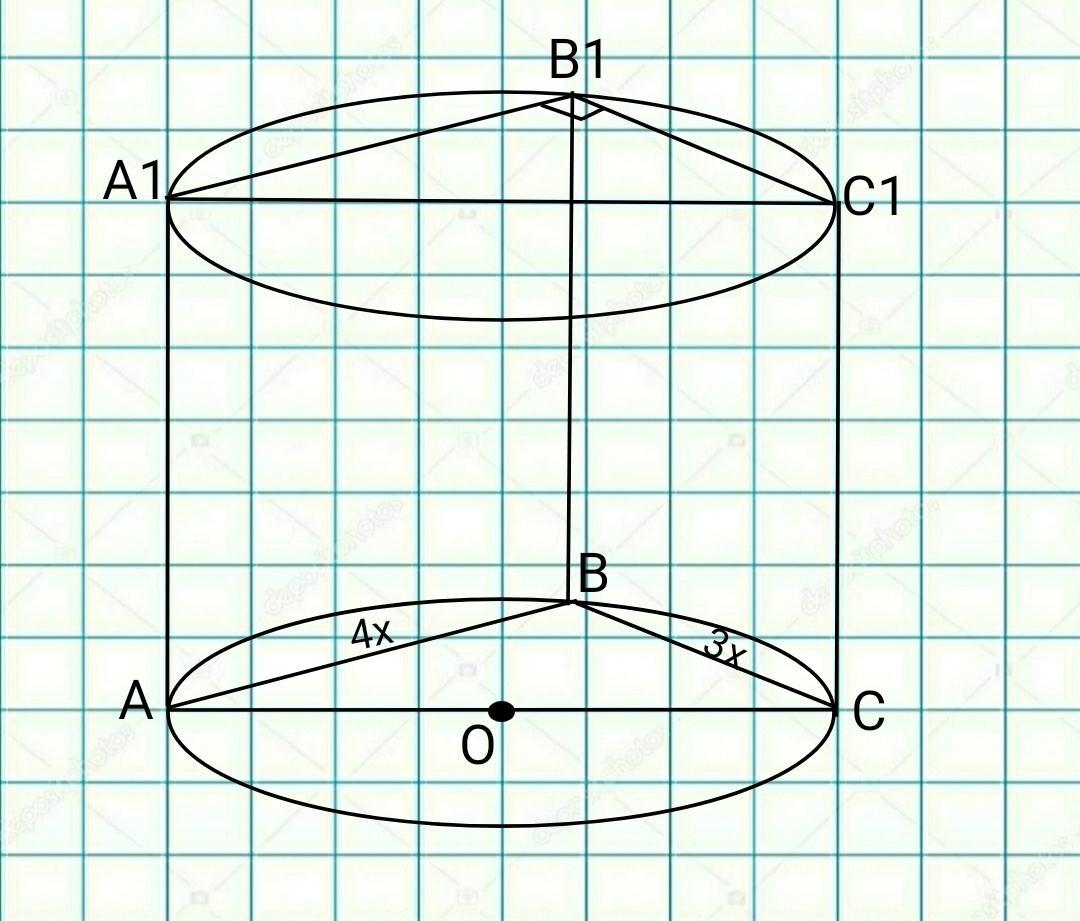
в цилиндр с радиусом 10 и площадью осевого сечения 100 вписана треугольная призма. основание призмы - прямоугольный треугольник, катеты которого относятся как 3:4. найдите объем призмы ​

Answer 1

Ответ:

V=180

Объяснение:

D=2R=2*10=20 диаметр цилиндра и гипотенуза прямоугольного треугольника.

АС=D=20

ВС:АВ=3:4

Пусть ВС будет 3х, а АВ будет 4х.

По теореме Пифагора АВ²+BC²=AC², составляем уравнение.

(3х)²+(4х)²=20²

9х²+16х²=400

25х²=400

х=√(400/25)

х=√16

х=4

ВС=3х=3*4=12

АВ=4х=4*4=16

S(∆АВС)=1/2*ВС*АВ=1/2*12*16=36 площадь основания призмы.

Sсеч=АА1*АС→

АА1=Sсеч/АС=100/20=5 высота цилиндра и высота призмы.

V=S(∆ABC)*AA1=36*5=180