Question

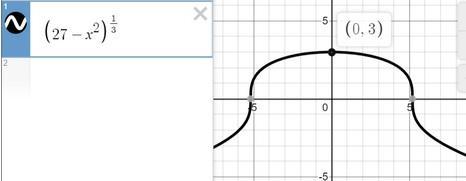
найдите координату x точки максимума функции y = (27-x^2) в степени 1/3

Answer 1

Ответ:

Пошаговое объяснение:

первая производная

$\displaystyle y'=\bigg ((27-x^2)^{1/3}\bigg )'=-\frac{2}{3} *\frac{x}{(27-x^2)^{2/3}} \\\\-\frac{2}{3} *\frac{x}{(27-x^2)^{2/3}} =0; \qquad \Rightarrow\quad x_1=0$

x₁ = 0 - это критическая точка, в ней есть экстремум функции

теперь посмотрим, это минимум или максимум

вторая производная

$\displaystyle y''=-\frac{8}{9} *\frac{x^2}{(27-x^2)^{5/3}}-\frac{2}{3} *\frac{2}{(27-x^2)^{2/3}}=\frac{-2x^2-162}{9(27-x^2)^{5/3}}$

смотрим знак второй производной в точке х₁ = 0

$\displaystyle y''(0)=-\frac{2}{27} <0$    

точка х₁ = 0 - точка максимума

f(0) = 3

ответ

координат0 x точки максимума функции = 0

Answer 2

Ответ:

(см. объяснение)

Пошаговое объяснение:

$y=\sqrt[3]{27-x^2}$

Под знаком корня парабола, ветви которой направлены вниз. Тогда ее наибольшее значение достигается в вершине. Значит наибольшее значение функции достигается при $x$ вершины параболы. Поэтому при $x=0$ значение функции максимально.

Задание выполнено!