Предмет: Геометрия,
автор: Сабина0609
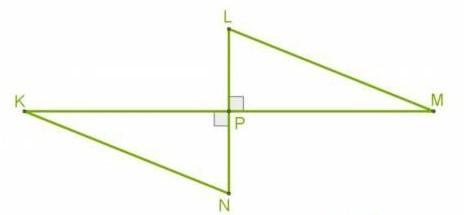
Два перпендикулярных отрезка KM и LN пересекаются в общей серединной точке P. Какой величины∡ N и ∡ K, если ∡ L = 20° и ∡ M = 70°?
1. Отрезки делятся пополам, значит, KP =(ответ),
(ответ) = LP, ∡ (ответ) = ∡ MPL, так как прямые перпендикулярны и оба угла равны (ответ) °.
По первому признаку равенства треугольник KPN равен треугольнику MPL.
2. В равных треугольниках соответствующие углы равны.
В этих треугольниках соответствующие ∡(ответ) и ∡ M, ∡(ответ) и∡ L. ∡ K =(ответ) °; ∡N=(ответ)°
Ответы
Автор ответа:
5
Ответ:
,.......,.........,
Объяснение:
1.
Отрезки делятся пополам, значит, KP=РМ,
PN=LP, угол КРN=углу MPL, так как прямые перпендикулярны и оба угла равны 90°.
По первому признаку равенства треугольник KPN равен треугольнику MPL.
2.
В равных треугольниках соответствующие углы равны.
В этих треугольниках соответствующие угол К и угол M, угол N и угол L. Угол К=70°; угол N=20°
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: умница237
Предмет: Русский язык,
автор: tkachevaalina0
Предмет: Русский язык,
автор: умница237
Предмет: Геометрия,
автор: ratushcorp