Предмет: Математика,
автор: fanartsman
Упростить тригонометрическое выражение:
Приложения:
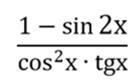
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: kateysha9
Предмет: Русский язык,
автор: kateysha9
Предмет: Українська література,
автор: Lena200008
Предмет: Алгебра,
автор: человек458
Предмет: Алгебра,
автор: mikkeyrurk