Предмет: Математика,
автор: vtina142005
sin²a + sin(60°+a)×sin(60°-a)
Приложения:
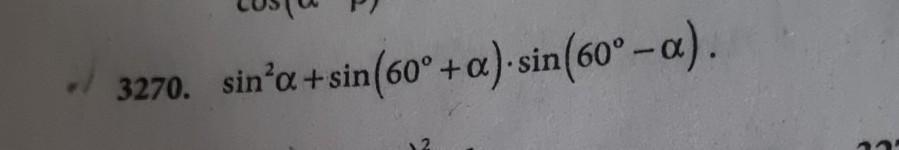
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Вспомним формулу синуса суммы/разности аргументов:
Применим эти формулы для наших углов
Вспомним формулу разности квадратов
Вспомним формулу
Вычислим
Автор ответа:
1
Ответ: 0,75
Пошаговое объяснение:
Применим формулу произведения синусов в сумму:
Откуда:
По формуле понижения степени:
Откуда:
Похожие вопросы
Предмет: Окружающий мир,
автор: олечка72
Предмет: Русский язык,
автор: fjdxnxhhj123
Предмет: Другие предметы,
автор: zebra30
Предмет: Русский язык,
автор: yanafun69