Предмет: Геометрия,
автор: GARRILA
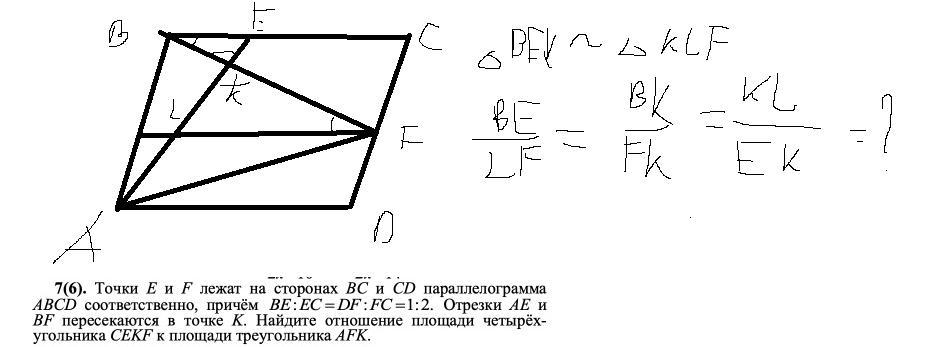
как найти lf ?если будет возможным помогите решить задачу
Приложения:
Ответы
Автор ответа:
1
Ответ:
5/6
Объяснение:
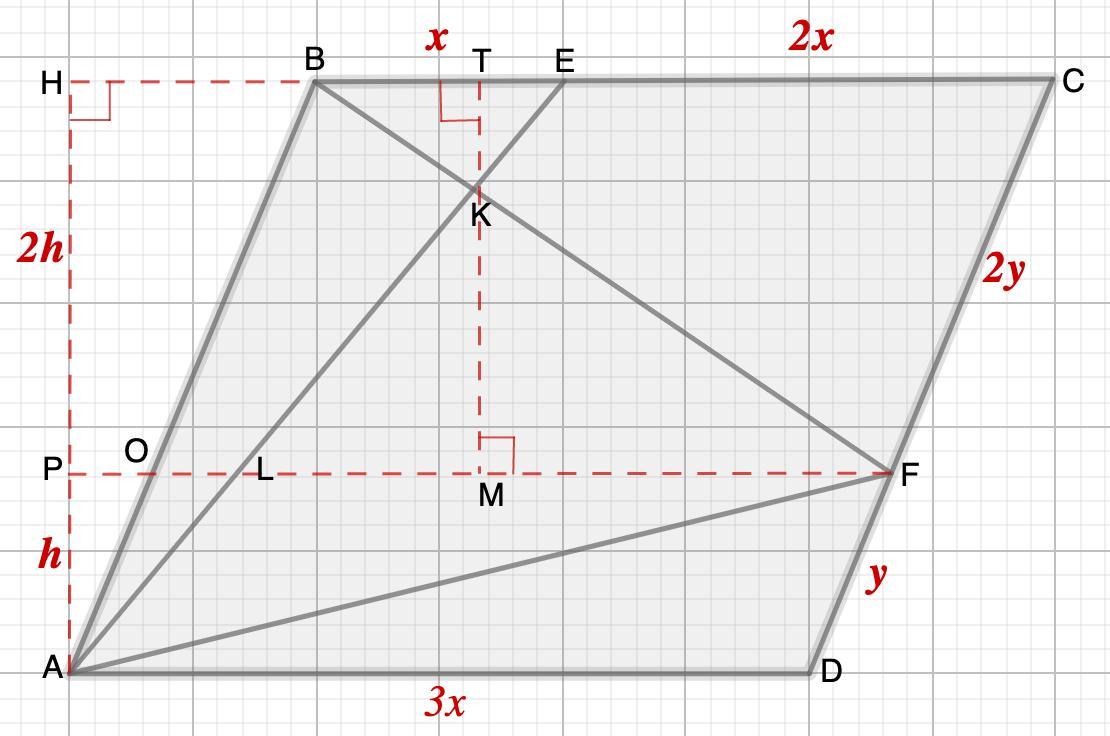
Доп. построение: PF║BC; AH - высота; ТМ⊥ВС.
1. (теорема о пропорциональных отрезках)
2.
3.
4.
5. Рассмотрим ΔAOL и ΔABE.
OL║BE⇒ΔAOL ~ ΔABE (лемма о подобии треугольников)
⇒
6. Рассмотрим ΔВЕК и ΔLKF
∠BKE=∠LKF (вертикальные)
∠КЕВ=∠KLF (накрест лежащие при ВЕ║LF и секущей EL)
⇒ ΔВЕК ~ ΔLKF
Высота подобных треугольников относятся как их стороны.
7.
8.
9.
10.
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: адалалс
Предмет: Английский язык,
автор: анна581
Предмет: Окружающий мир,
автор: лара0808
Предмет: Математика,
автор: artem01731
Предмет: Математика,
автор: ДеловойПомощник