Предмет: Геометрия,
автор: max7713817Max
Даю 50 балів . Скласти рівняння лінії , кожна точка якої задовольняє вказану умову:
Відношення відстаней від точки M до точок A (-3;5) i B(4;2) дорівнює 1/3.
Ответы
Автор ответа:
0
Даны точки A (-3;5) и B(4;2).
Примем координаты точки М(х; у).
Вектор АМ = ((х + 3); (у - 5)), вектор ВМ = ((х - 4); (у - 2)),
Длина АМ = √(((х + 3)² + (у - 5)²) = √(x² + 6x + 9 + y² - 10y + 25),
Длина BМ = √(((х - 4)² + (у - 2)²) = √(x² - 8x + 16 + y² - 4y + 4).
По условию задания:
3*√(x² + 6x + y² - 10y + 34) = √(x² - 8x + y² - 4y + 20).
Возведём в квадрат.
9*(x² + 6x + y² - 10y + 34) = x² - 8x + y² - 4y + 20.
9x² + 54x + 9y² - 90y + 306 = x² - 8x + y² - 4y + 20.
8x² + 62x + 8y² - 86y + 286 = 0.
Сократим на 8.
x² + (31/4)x + y² - (43/4)y + (143/4) = 0.
Выделим полные квадраты и получаем уравнение окружности:
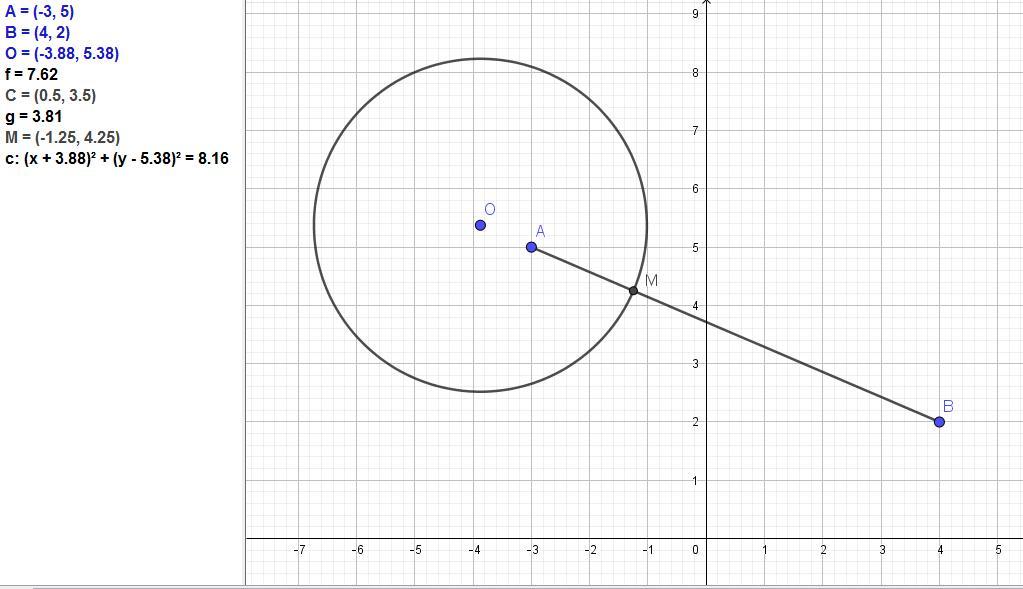
(x + (31/8))² + (y - (43/8))² = 261/32.
Центр окружности О = (-31/8); (43/8)), радиус R = 2,855915.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: olegkitsyn04
Предмет: Русский язык,
автор: linamila20151
Предмет: Русский язык,
автор: что111234561
Предмет: Английский язык,
автор: zed1111122