Помогите решить!!! СРОЧНО!!!! !
Задача:
Стеклянная двояковогнутая линза с оптической силой 3,33 дптр отстоит от предмета на расстоянии 0,2 м. Нарисовать ход лучей с соблюдением масштаба и определите расстояние от линзы до изображения. Как изменится ход лучей и где будет изображение, если линзу и предмет поместить в сероуглерод?
Ответы
Дано:
n_линзы = n₁ = 1,5
D = 3,33 дптр
d = 0,2 м
n_сероуглерода = n₂ = 1,63
f, f' - ?
Решение:
Линза - двояковогнутая, а значит её фокус является мнимым. Следовательно, оптическая сила линзы - отрицательная:
1/|-F| = D => 1/(-F) = -D
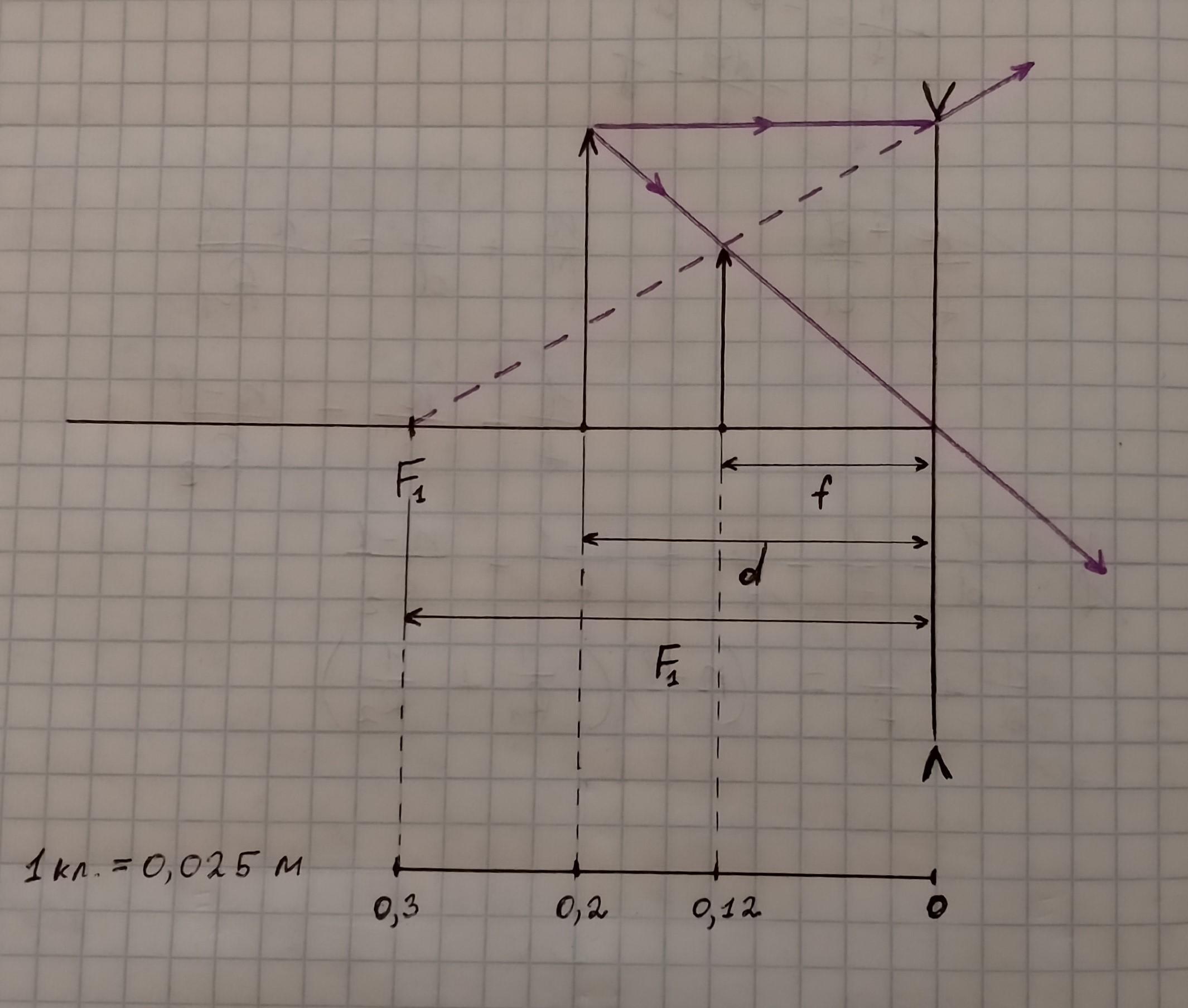
Изображение предмета будет мнимым, прямым и уменьшённым (см. рисунок). Оно будет находится ближе к линзе, чем предмет (в случае с рассеивающей линзой такая ситуация выполняется при любых расстояниях между предметом и линзой). Т.к. изображение мнимое, то расстояние f - тоже отрицательная величина. Найдём его по формуле тонкой линзы.
Когда мы ищем какую-то величину, мы ставим перед ней знак "+", даже если знаем, что она является отрицательной:
1/d + 1/f = -1/F = -D
1/f = -D - 1/d = -Dd/d - 1/d = -(Dd + 1)/d =>
=> f = -d/(Dd + 1) = -0,2/(3,33*0,2 + 1) = -0,12004... = -0,12 м
f = -0,12 м
Теперь поместим линзу и предмет в сероуглерод. Углеродная среда является оптически более плотной, чем стекло. Поэтому лучи, идущие через линзу, будут преломляться к её центру, а не от него, как это происходит в случае рассеивающей линзы, находящейся в воздухе. То есть, другими словами, рассеивающая линза станет собирающей, а значит её фокус окажется положительным. Обозначим фокус F как F₁.
Найдём новый фокус линзы F₂, используя общую формулу для оптической силы линзы:
D = 1/F = (n - 1)*(1/R₁ + 1/R₂), где
n - относительный показатель преломления, равный:
n = n_линзы/n_среды
R₁ и R₂ - радиусы кривизны сферических поверхностей, которыми ограничена линза
Мы не знаем R₁ и R₂. Всё, что мы можем предположить, так это то, что радиусы равны друг другу, потому что мы рассматриваем симметричную линзу. Тогда:
R₁ = R₂ = R
1/F = (n - 1)*(1/R + 1/R) = (n - 1)*(2/R) =>
=> F = R/(2*(n - 1))
Для F₁ и F₂:
F₁ = R/(2*(n - 1)), где n = n₁/n_воздуха, но т.к. n_воздуха = 1, то n = n₁ =>
=> F₁ = R/(2*(n₁ - 1))
F₂ = R/(2*(n' - 1)) = R/(2*(n₁/n₂ - 1))
Не забываем, что фокус рассеивающей линзы в воздухе является отрицательным. Есть правило: когда поверхность линзы выпуклой стороной смотрит в менее плотную среду, то радиус кривизны положителен, когда наоборот - отрицателен. Наша линза - вогнутая с двух сторон. Но правило применимо и к ней: вогнутость - это обратная выпуклость. И в случае воздуха, который оптически менее плотен, чем стекло линзы, эта обратная выпуклость смотрит на стекло - более плотную среду, чем воздух. Значит, радиус кривизны отрицателен. В случае сероводорода - положителен. Поэтому перед R в выражении F₁ поставим знак "-". Либо его можно поставить перед самим F₁. Но нельзя ставить и там и там - результат получится ошибочным. Поделим F₁ на F₂:
F₁/F₂ = -R/(2*(n₁ - 1)) / R/(2*(n₁/n₂ - 1)) = -(n₁/n₂ - 1) / (n₁ - 1) = (1 - n₁/n₂) / (n₁ - 1)
Выражаем F₂:
F₂ = F₁ / ((1 - n₁/n₂) / (n₁ - 1)) = F₁*(n₁ - 1)/(1 - n₁/n₂) = (1/D)*(n₁ - 1)/(1 - n₁/n₂) = (1/3,33)*(1,5 - 1)/(1 - 1,5/1,63) = 1,88265... = 1,89 м - фокусное расстояние довольно сильно увеличилось.
Т.к. предмет мы оставили на прежнем расстоянии от линзы, то её изображение при изменённом фокусе будет находится на расстоянии:
1/d + 1/f' = 1/F₂
1/f' = 1/F₂ - 1/d = (d - F₂)/(F₂*d)
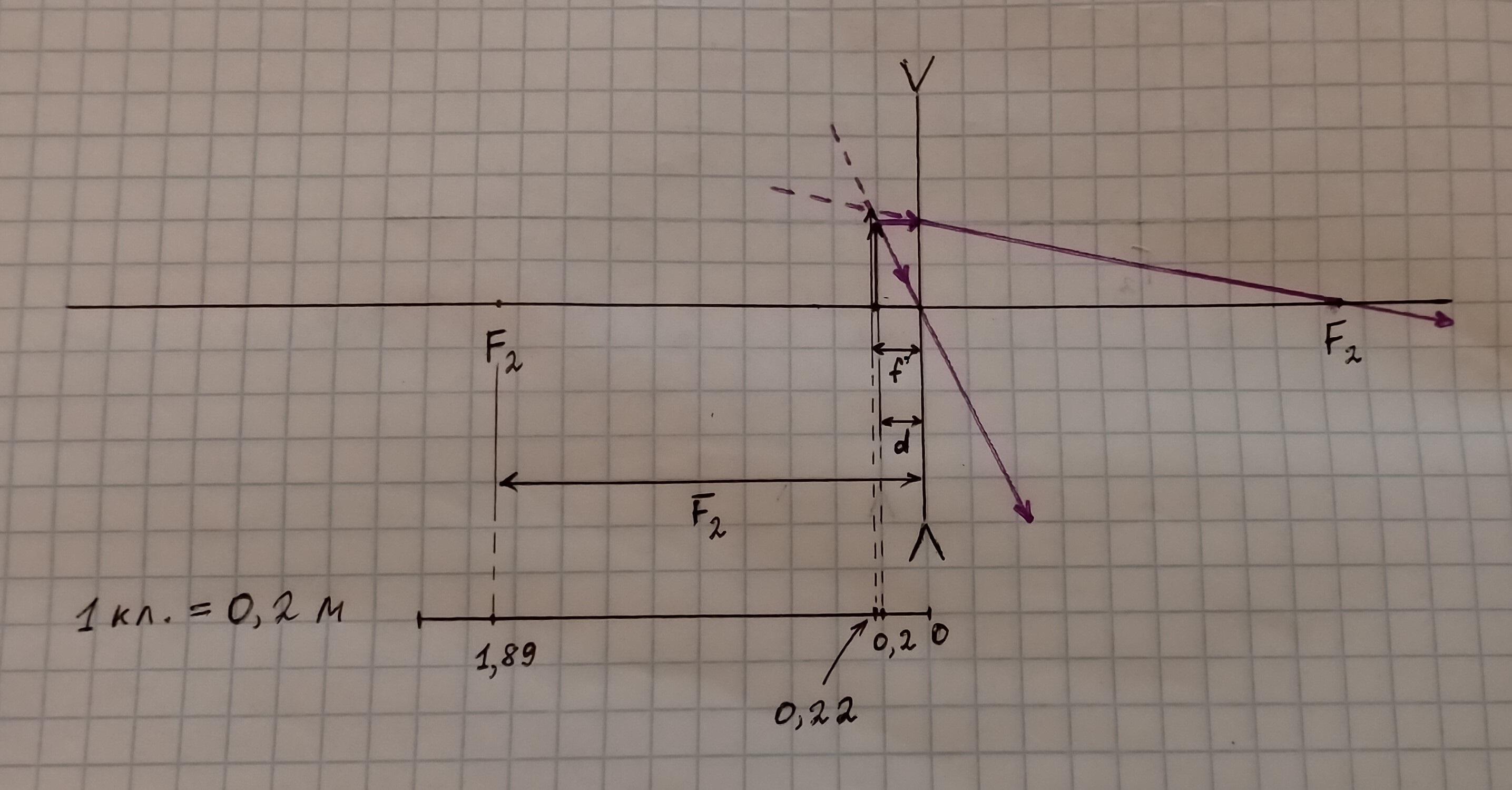
f' = F₂*d/(d - F₂) = 1,89*0,2/(0,2 - 1,89) = -0,22366... = -0,22 м
f' = -0,22 м - изображение получается мнимым, находится дальше от линзы, чем предмет. Кроме того, оно прямое и увеличенное (см. рисунок). Всё так, как в случае собирающей линзы, когда предмет находится на расстоянии от неё, меньшем фокусного.
Итог:
В воздухе двояковогнутая линза рассеивает лучи, изображение предмета всегда получается мнимым, прямым и уменьшённым.
В сероуглеродной среде двояковогнутая линза собирает лучи, т.к. оптическая плотность сероуглерода больше, чем оптическая плотность стекла. При том же расстоянии между предметом и линзой изображение выходит мнимым, прямым и увеличенным.