Предмет: Математика,
автор: sanyakozel28
Помогите пожалуйста срочно
Приложения:
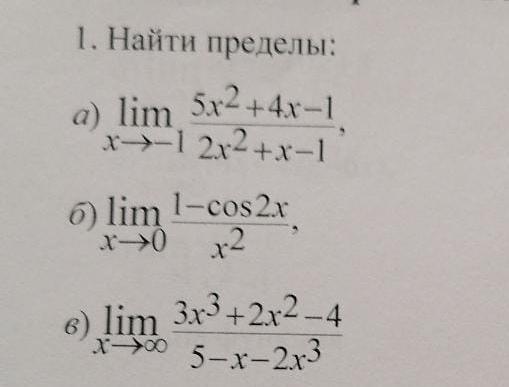
Ответы
Автор ответа:
1
Ответ:
а) 2
б) 2
в) -1,5
Пошаговое объяснение:
а)
Разложим числитель и знаменатель на множители, решив соответствующие квадратные уравнения:
Теперь можем сократить дробь на множитель, равный нулю при x = -1:
б)
Здесь я воспользовался первым замечательным пределом:
в)
Похожие вопросы
Предмет: Окружающий мир,
автор: PusheenCat1
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: 11111177
Предмет: Математика,
автор: mukan20051
Предмет: Русский язык,
автор: ааааарррттт