Предмет: Геометрия,
автор: sofija91
Помогите решить! В треугольнике проведены две высоты AA1 и СС1. А1НВС1-вписанный четырехугольник (Н-ортоцентр). М-середина АС. Нужно доказать, что МС1 и МА1-касательные к окружности.
cos20093:
Ну, точки M, A1, C1 и E - середина BH лежат на окружности Эйлера, и там же лежит B1 - основание высоты BB1. Угол BB1M прямой, => EM диаметр окружности Эйлера. => углы MA1E и MC1E прямые. При этом E - центр окружности (A1BC1H) (надо объяснять?), EA1 и EC1 - радиусы этой окружности. => MA1 и MC1 касательные к ней.
Для тех, кому интересно. Есть много способов показать, что 9 точек любого треугольника - середины сторон, основания высот и середины отрезков между вершинами и ортоцентром - лежат на одной окружности.
Лично мне нравится такой - 1. надо доказать, что точки, симметричные ортоцентру относительно сторон и середин сторон (всего 6 точек) лежат на описанной окружности. 2. при гомотетии с центром в ортоцентре и коэффициентом 1/2 описанная окружность перейдет в другую окружность, которая пройдет через середины сторон и основания высот. Три другие точки будут бонусом, также как и положение центра окружности Эйлера.
Можно поискать среди моих решений, это там есть.
Ответы
Автор ответа:
2
Ладно, пусть будет, задачка простенькая и полезная для общего образования.
Отрезок BH - диаметр заданной в задаче окружности (A1BC1H), так как углы BA1H и BC1H прямые. Пусть E - середина BH, то есть центр окружности (A1BC1H). EA1 и EC1 - радиусы этой окружности.
Точки M, A1, C1 и E лежат на окружности Эйлера, и там же лежит B1 - основание высоты BB1. Угол BB1M прямой, => EM диаметр окружности Эйлера => углы MA1E и MC1E прямые => MA1 и MC1 касательные к окружности (A1BC1H).
Приложения:
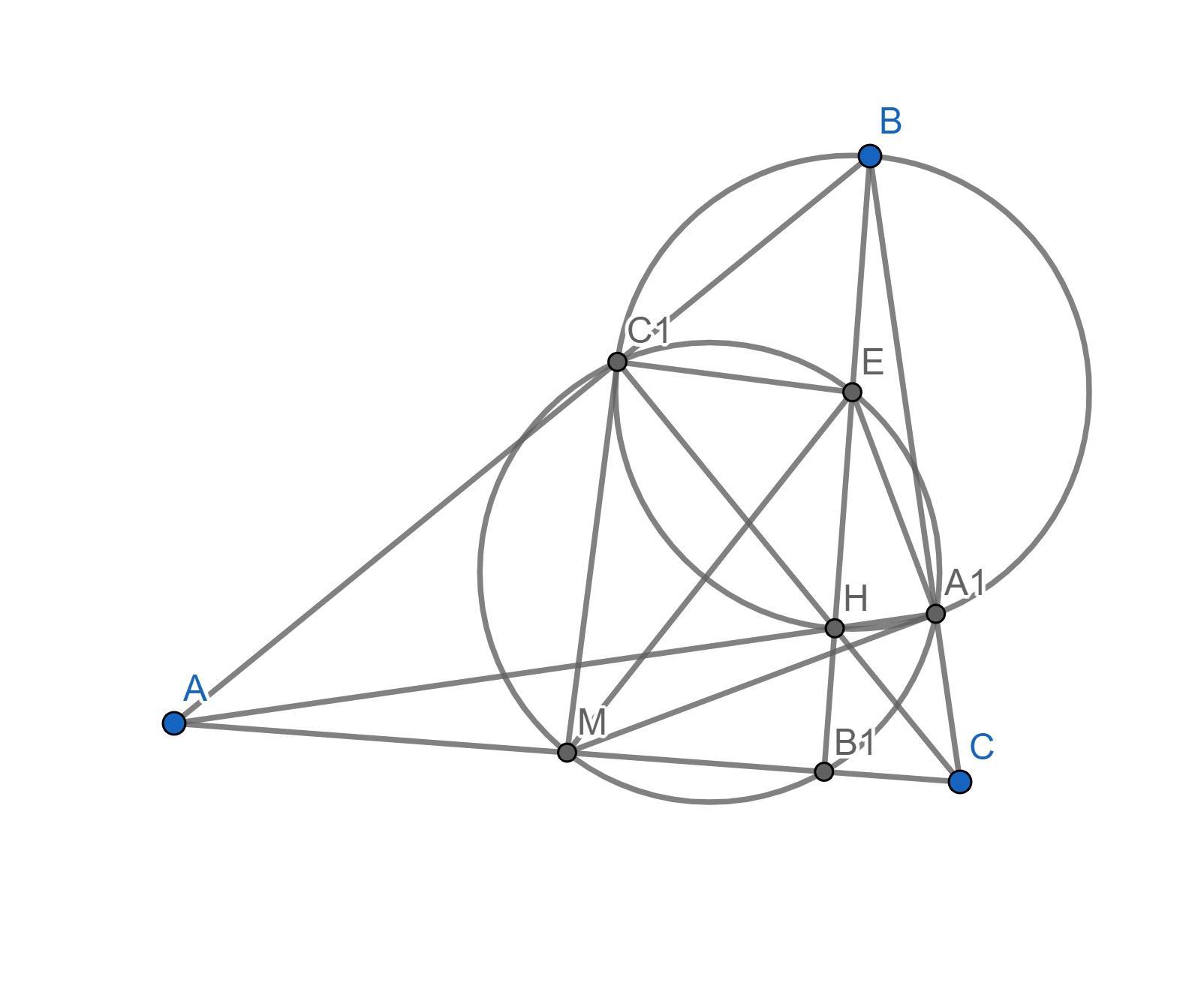
Почему Е-центр окружности, описанного вокруг 4-угольника A1BC1H?
середина диаметра
Похожие вопросы
Предмет: Другие предметы,
автор: sahuly1222
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Лана165998
Предмет: Математика,
автор: LuCkY1111111111h
Предмет: Математика,
автор: anastasiar3