Предмет: Математика,
автор: ksolongin
Решите карточку по математике:
Приложения:
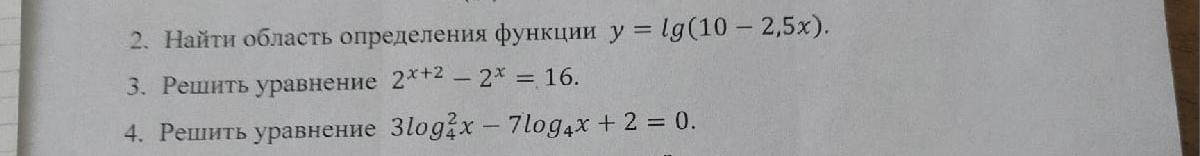
Ответы
Автор ответа:
1
Ответ:
2) x∈(-∞; 4)
3) x = 4-log2 (3)
4) x ∈ {4^(1/3); 16}
Пошаговое объяснение:
2) Логарифмическая функция определена на множестве положительных чисел.
3)
4)
ksolongin:
Спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: pyfybt1
Предмет: Русский язык,
автор: jylayka
Предмет: Английский язык,
автор: Аноним
Предмет: Русский язык,
автор: denik20074
Предмет: Английский язык,
автор: karanet