Предмет: Математика,
автор: akunamatata53999
Найдите точку минимума функции, решить подробно
Приложения:
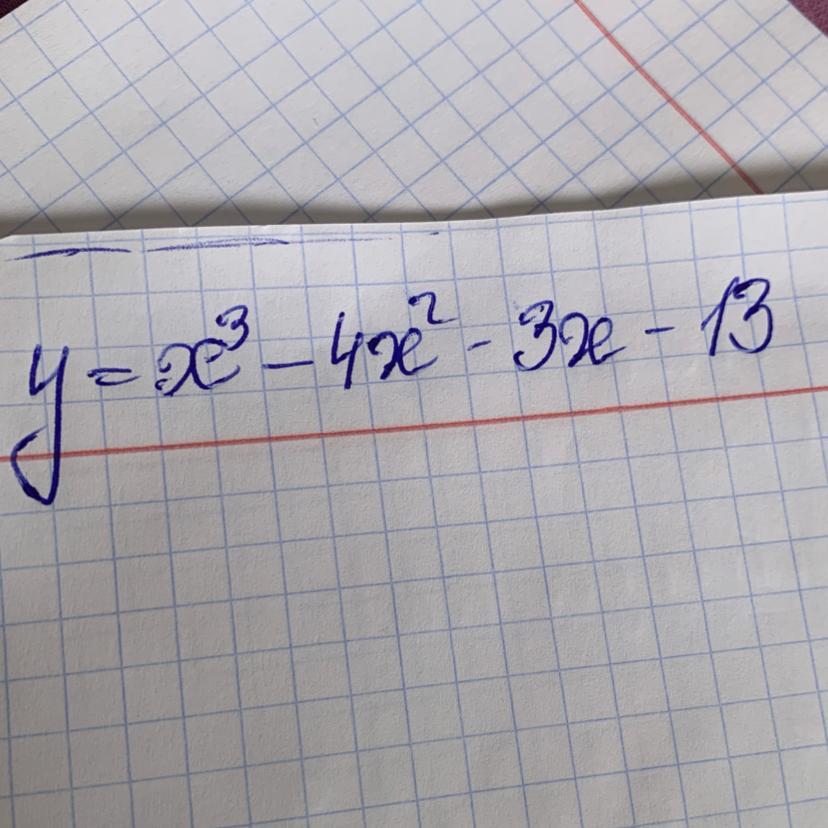
Ответы
Автор ответа:
2
Производная y' = 3x² – 8x – 3. Приравняем производную к нулю, найдем экстремумы и промежутки монотонности:
3x² – 8x – 3 = 0
D = (–8)² + 4·3·3 = 100 = 10²
x₁ = (8 – 10) / 6 = –1/3
x₂ = (8 + 10) / 6 = 3
Производная отрицательна на интервале (–1/3; 3), поэтому функция на этом интервале убывает и достигает локального минимума при x = 3.
y(3) = 3³ – 4·3² – 3·3 – 13 = 27 – 36 – 9 – 13 = –31
Ответ: локальный минимум достигается в точке (3; –31).
akunamatata53999:
Как получили 8 х?
Дифференцированием: (4x²)’ = 8x
Автор ответа:
1
Ответ: хmin=3, уmin=27-36-9-13=-31, см фото
Пошаговое объяснение:
Приложения:

Как получили 8 х?
Похожие вопросы
Предмет: Русский язык,
автор: ZilkaDilka
Предмет: Қазақ тiлi,
автор: Тормоз11
Предмет: Английский язык,
автор: sokruto31
Предмет: Математика,
автор: antomimik
Предмет: Математика,
автор: Аноним