Предмет: Алгебра,
автор: mnogodeneg228
РЕБЯТ!!!!! ПОМОГИТЕ ПОЖАЛУЙСТА ОЧЕНЬ СРОЧНО!!!!! помогите решить это:
Приложения:
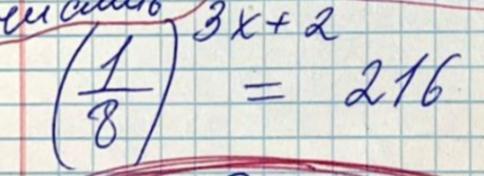
mnogodeneg228:
Тоже так думал, но Учитель так написал, может ошибся.
Ответы
Автор ответа:
0
Объяснение:
Извини за почерк, там в конце надо доделить на 3, чтобы получилось х=
Приложения:
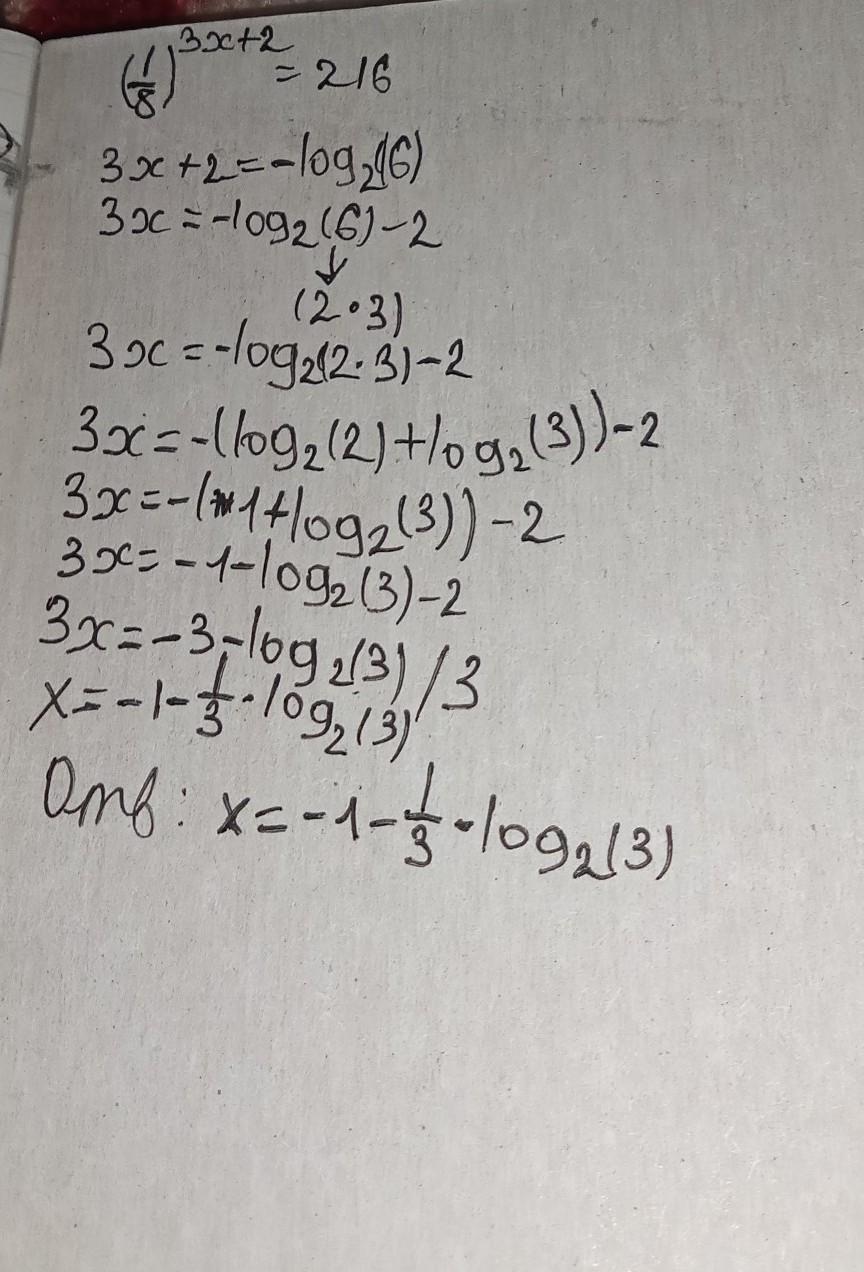
Подробные решения, я делал в уме
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Другие предметы,
автор: МультаиНазар
Предмет: Английский язык,
автор: Аноним
Предмет: Қазақ тiлi,
автор: DiasAska
Предмет: Русский язык,
автор: ayanych
Предмет: Биология,
автор: Аноним