Предмет: Математика,
автор: sadvh6
Помогите решить
..........
Приложения:
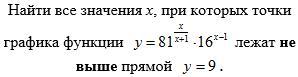
Ответы
Автор ответа:
1
Ответ:
Пошаговое объяснение:
Необходимо решить следующее неравенство:
- + - +
--------*---------o-----*----->
-1-log₄3 -1 1 x
Похожие вопросы
Предмет: Русский язык,
автор: 1234567866
Предмет: Окружающий мир,
автор: уевль
Предмет: Русский язык,
автор: maria727272
Предмет: Русский язык,
автор: амина780