Предмет: Математика,
автор: niceguy0
Вычислить определенный интеграл 70 баллов
Приложения:
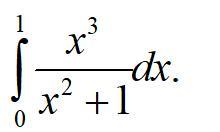
Ответы
Автор ответа:
1
Ответ:
0,5×(1-ln2)
Пошаговое объяснение:
Похожие вопросы
Предмет: Английский язык,
автор: vika228destro
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: никита1234650986443
Предмет: Математика,
автор: дон57
Предмет: Окружающий мир,
автор: tatynab577p7qyjg