Предмет: Математика,
автор: dianatihonenko678
Помогите решить пожалуста!)
Приложения:

Ответы
Автор ответа:
1
интегралы:
площадь:
Приложения:
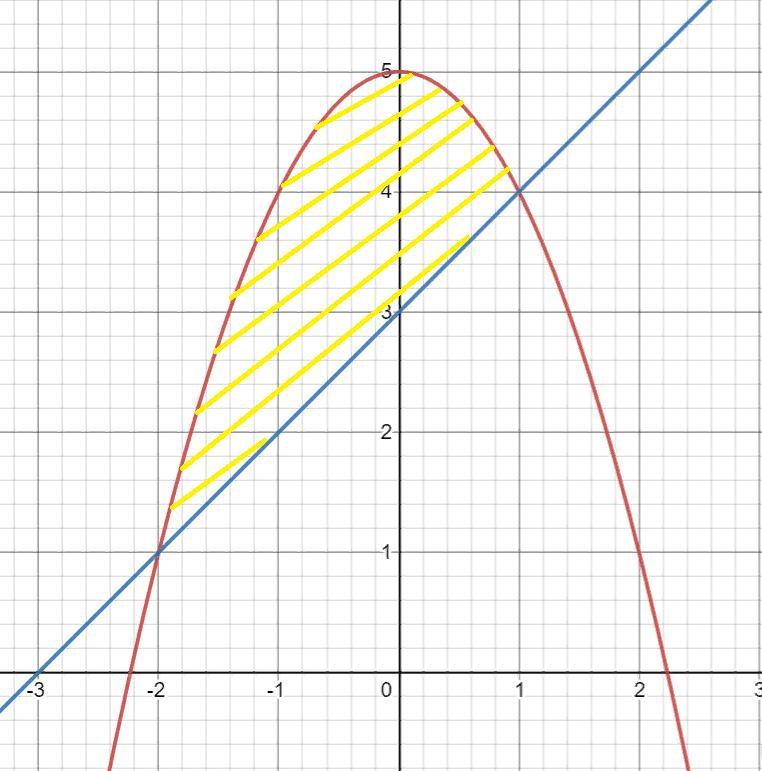
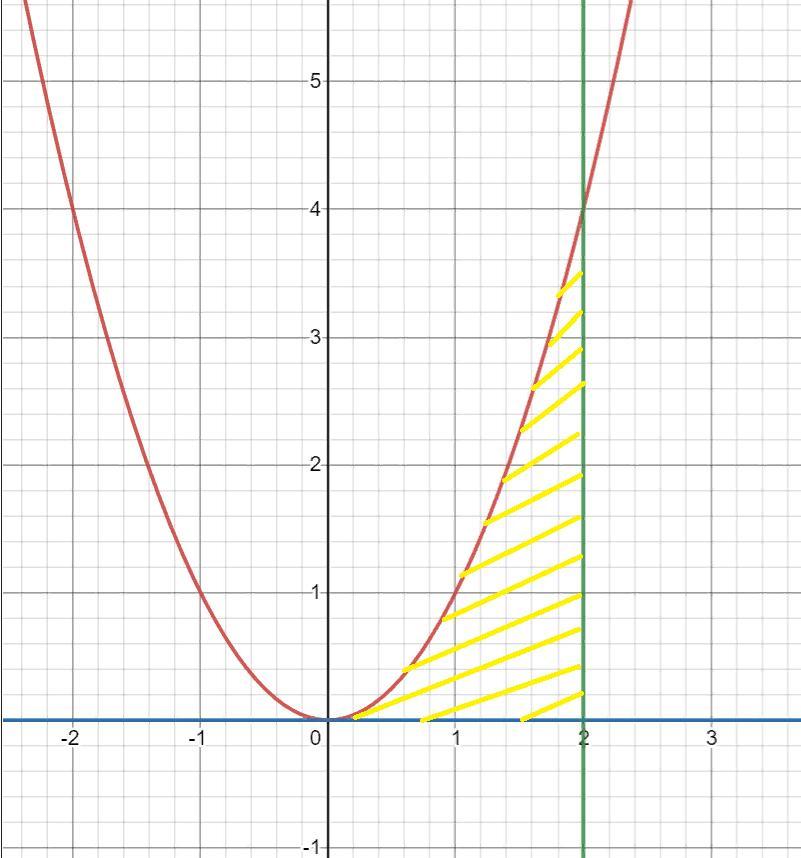
dianatihonenko678:
спасибо)
ошибся со 2 интегралом(площадь) и уже исправил
Похожие вопросы
Предмет: Английский язык,
автор: annaneustroeva
Предмет: Русский язык,
автор: Link11111
Предмет: Русский язык,
автор: Зухра11111
Предмет: Українська мова,
автор: nns77p19iwo
Предмет: Математика,
автор: mark192