Предмет: Алгебра,
автор: artyompushkarev0000
1. Решите систему неравенств: 2x > 8
3x > 81
(1;4)
(4;5)
(2;3)
(3;4)
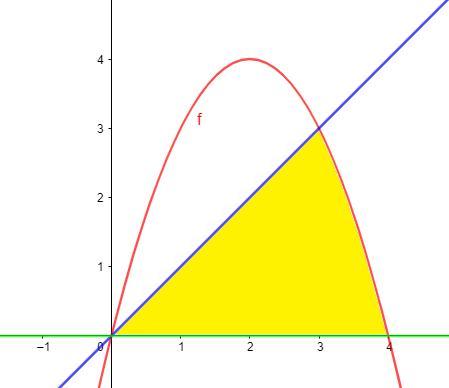
2. Площадь фигуры, ограниченной линиями y=4x-x^2, y=x, y=0, равна
13/3
8/3
9/2
13/6
3. Найдите функцию, обратную данной функции y=3x-7
y = x/3 + 7
y = x/3 + 3
y = x/3 + 7/3
y = x+ 7/3
4. составить уравнение прямой проходящей через точку (12; -5), перпендикулярно прямой y = 2x -5
y = -2x -5
y = 0,5x + 1
y = -4x + 1
y = -0,5x +14
Ответы
Автор ответа:
2
Ответ:
1.
2.
3.
4.
Объяснение:
1.
2.
или y = x
3.
Обратная функция:
4.
A(12; -5)
y = 2x - 5
Пусть , а
- угловой коэффициент прямой уравнение которой надо составить. Так как по условию прямые перпендикулярны, то по теореме:
.
y = kx + b ⇒ b = y - kx = -5 - (-0,5) * 12 = -5 + 6 = 1
y = -0,5x + 1
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: дарья650
Предмет: Қазақ тiлi,
автор: мааргарита
Предмет: Русский язык,
автор: Evgsolnce
Предмет: Математика,
автор: Аноним