Question

вычислите площадь фигуры, ограниченной линиями​

Answer 1

Ответ: 1 1/3.

Объяснение:

Решение.

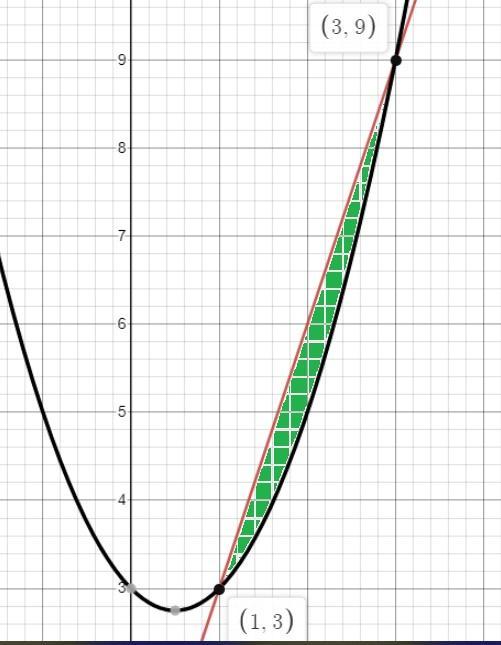
Построим графики функций

y=x²-x+3; y=3x.

Пределы интегрирования видно по графикам функций от 1 до 3.

См. скриншот.

----------

S=∫₁³3x-(x²-x+3)dx=∫₁³(3x-x²+x-3)dx= ∫₁³(4x-3-x²)dx=

=4∫₁³xdx-3∫₁³dx-∫₁³x²dx=4/2x²|₁³-3x|₁³-1/3x³|₁³=

=(2*9-3*3-1/3*27)-(2-3-1/3)=0-(-4/3)=1  1/3.