Question

Исследовать функцию и построить ее график (НОМЕР 18)

Answer 1

Ответ:

↓↓↓

Пошаговое объяснение:

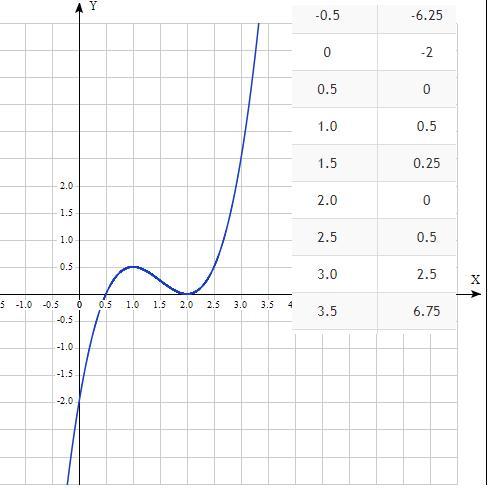
у=х³-9\2*х²+6х-2

у=х³-4,5х²+6х-2. Область определения х-любое.

1)Промежутки возрастания и убывания.

Найдем производную функции  

у'=(х³-4,5х²+6х-2)'=3х²-9х+6=3(х²-3х+2)=3(х-2)(х-1).

Критические точки х=2,х=1 , при у'=0. Функция возрастает  если  у'>0  

3(х-2)(х-1)>0  

++++++++++(1)- -- -- -- - -- -(2)++++++++ ,   х∈(-∞;1) и (2;+∞) .

Т.к. функция определена и непрерывна при любом х, то можно включит концы отрезка х∈(-∞;1]  и [2;+∞)

Функция убывает если  у'<0   ⇒ х∈[1;2]  .

2)Экстремумы функции у=х³-4,5х²+6х-2.  

у'          +                                 -                          +

-----------------------(1)---------------------------(2)---------------

у     возр           max            убыв       min        возр

х=1 точка максимума , у(1)=1³-4,5*1²+6*1 -2=1- 4,5+6-2=0,5

х=2  точка минимума  ,   у(2)=2³-4,5*2²+6*2 -2= 0.