Question

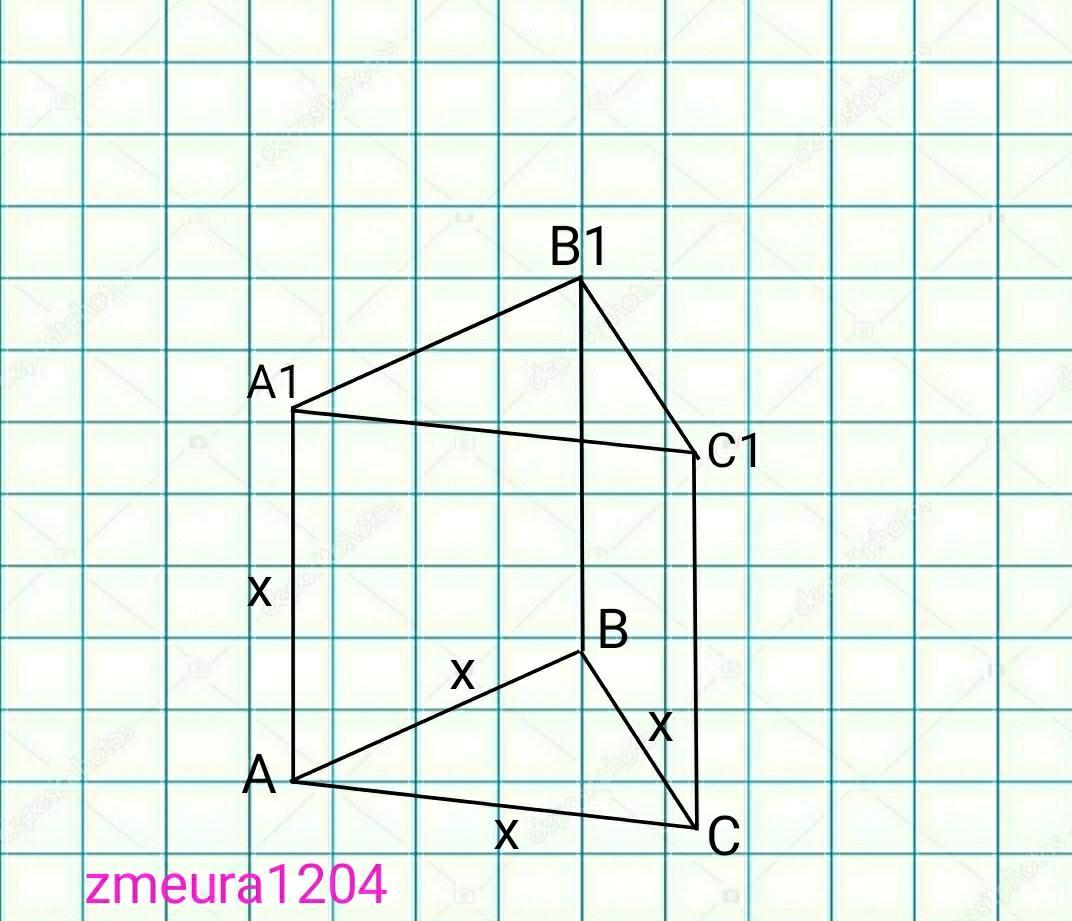
Все ребра прямой треугольной призмы имеют одинаковую длину. Площадь полной поверхности призмы равна$12+24\sqrt{3}$. Найдите площадь основания призмы.
Помогите плз. Дано решение
ответ вроде должен быть 6

Answer 1

Ответ:

Sосн=6

Объяснение:

Дано:

АВСА1В1С1-правильная призма.

∆АВС- равносторонний треугольник

Sпол=12+24√3

Sосн=?

Решение.

Все ребра одинаковые

АВ=ВС=АС=АА1=ВВ1=СС1=А1В1=В1С1=А1С1;

Пусть каждое ребро будет иметь значение х.

Формула нахождения площади боковой поверхности.

Sбок=Росн*h.

Росн=3*АВ=3х

h=x

Sбок=3х*х=3х²

Формула нахождения равностороннего треугольника ∆АВС.

Sосн=АВ²√3/4; АВ=х

Sосн=х²√3/4.

Формула нахождения площади полной поверхности призмы.

Sпол=Sбок+2*Sосн.

Sпол=3х²+2*х²√3/4=3х²+х²√3/2.

Составляем уравнение

3х²+х²√3/2=12+24√3 умножаем правую и левую часть на 2.

6х²+х²√3=24+48√3

х²(6+√3)=24+48√3

х²=(24+48√3)/(6+√3)

х²=(24(1+2√3)/(√3(2√3+1) сокращаем на (1+2√3)

х²=24/√3

х²=8*√3*√3/√3

х²=8√3.

Подставим значение х² в формулу площадь основания.

Sосн=x²√3/4=8√3√3/4=2*3=6