4. У шестиугольника с одинаковыми углами , но не одинаковыми сторонами,
площадь в 3 раза больше правильного шестиугольника со стороной 1 .
Если все длины сторон целые числа , чему равен периметр большего
шестиугольника?

Ответы
Ответ: P = 12
Объяснение:
Возможны другие варианты (ну, со сторонами а,а,в,с,с,д) но исследовать стало лень.
Так что бы все 6 сторон были неравными при углах 120 градусов не может быть (кажется :))

Ответ:
P=12
Объяснение:
Поскольку стороны искомого шестиугольника целочисленные, а углы 120, будем решать на сетке из единичных равносторонних треугольников (ед.).
Правильный шестиугольник со стороной 1 состоит из 6 ед., искомый шестиугольник - из 18 ед.
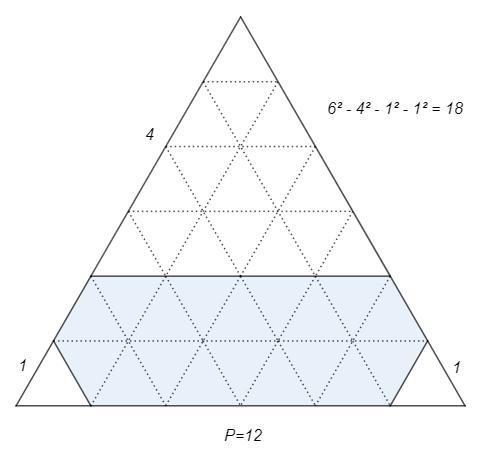
Искомый шестиугольник виден, его периметр 12.
Попробуем доказать перебором, что он единственный.
Любой шестиугольник с углами 120 (внешние углы 60) можно достроить до равностороннего треугольника, продлив стороны.
Количество ед., из которых состоит равносторонний треугольник, равно квадрату его стороны (сумма последовательных нечетных чисел равна квадрату).
От равностороннего треугольника со стороной t нужно отсечь равносторонние треугольники со сторонами a, b, c и получить площадь 18 ед.
t^2 -a^2 -b^2 -c^2 =18
Из рисунка видно, что t не может быть больше 6 (фигура высотой 1 ед. будет параллелограммом или трапецией, но не шестиугольником).
Перебирая квадраты целых чисел, находим единственное решение:
6^2 -4^2 -1^2 -1^2 =18