Предмет: Математика,
автор: termitor960
13-ое задание из профиля ЕГЭ. Решите, пожалуйста! Мне важен ответ.
Приложения:
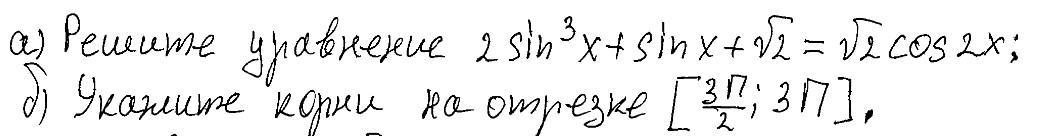
MrSolution:
cos2x разложите через синус, делаете замену, получаете ответ
Ответы
Автор ответа:
1
Ответ:
а)
б)
Пошаговое объяснение:
а)
или
б) Отберём корни с помощью тригонометрической окружности (см. рис.)
Подходят корни
Приложения:
Автор ответа:
0
Ответ:
а)
n∈Z
б)
Пояснение:
№13(а)
Произведение равно нулю,когда хотя бы один из множителей равен нулю
1)
n∈Z
2)
n∈Z
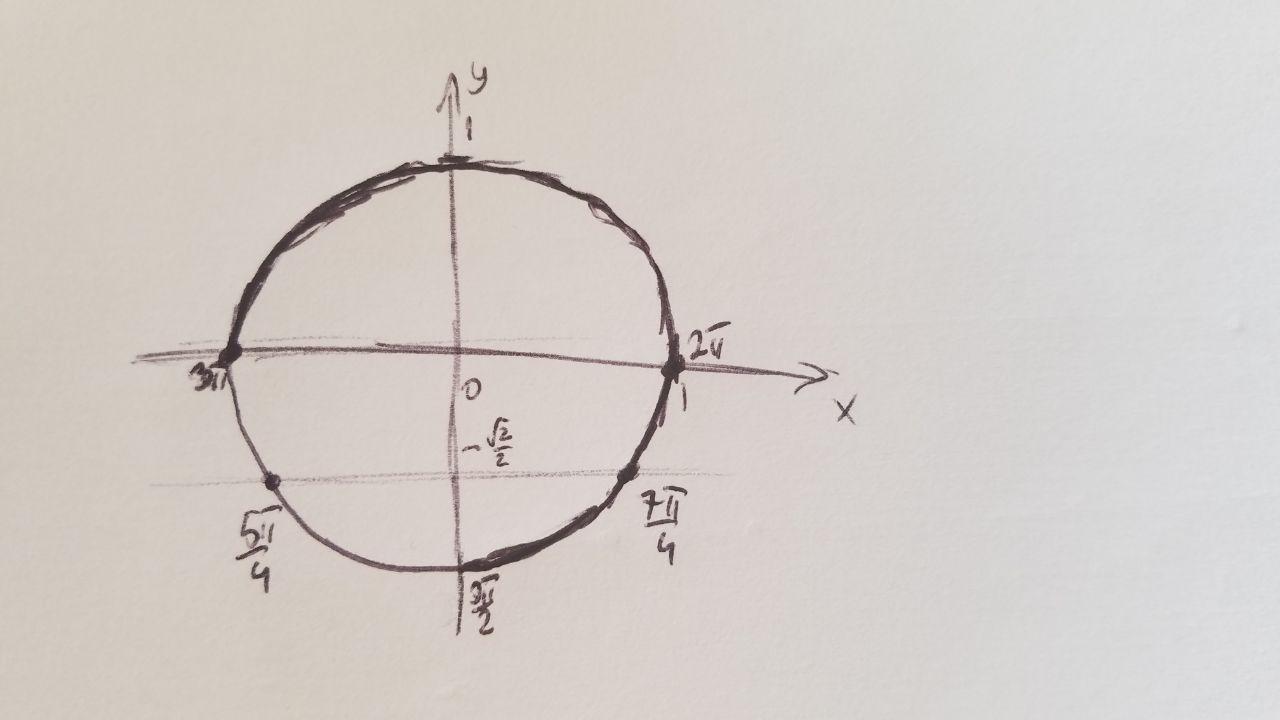
б) Найдем корни уравнения,принадлежащие отрезку [3п/2;3п], с помощью тригонометрической окружности(см. вложение)
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: evekentevi
Предмет: Английский язык,
автор: fas6
Предмет: Английский язык,
автор: Аделина20004
Предмет: Математика,
автор: Islam20099
Предмет: Английский язык,
автор: Аноним