Предмет: Алгебра,
автор: davidbru
Найдите промежутки возрастания и убывания и точки экстремума функции: f(x)=(x+1)^4(x-5)^3
Ответы
Автор ответа:
0
1) Находим первую производную:
f'(x) = 3*(x + 1)^4*(x - 5)^2 + 4*(x + 1)^3*(x - 5)^3
2) Приравниваем её к нулю и находим корни:
3*(x + 1)^4*(x - 5)^2 + 4*(x + 1)^3*(x - 5)^3 = 0
Корни:
x1 = -1
x2 = 17/7
x3 = 5
3) Отмечаем на числовой прямой, находим на промежутках знак функции (если знак +, то функция возрастает (стрелочка вверх) ; если знак - , то убывает(стрелочка вниз))
Точка -1 - максимум так как знак меняется с + на -
Точка 17/7 - минимум так как знак меняется с - на +
Приложения:
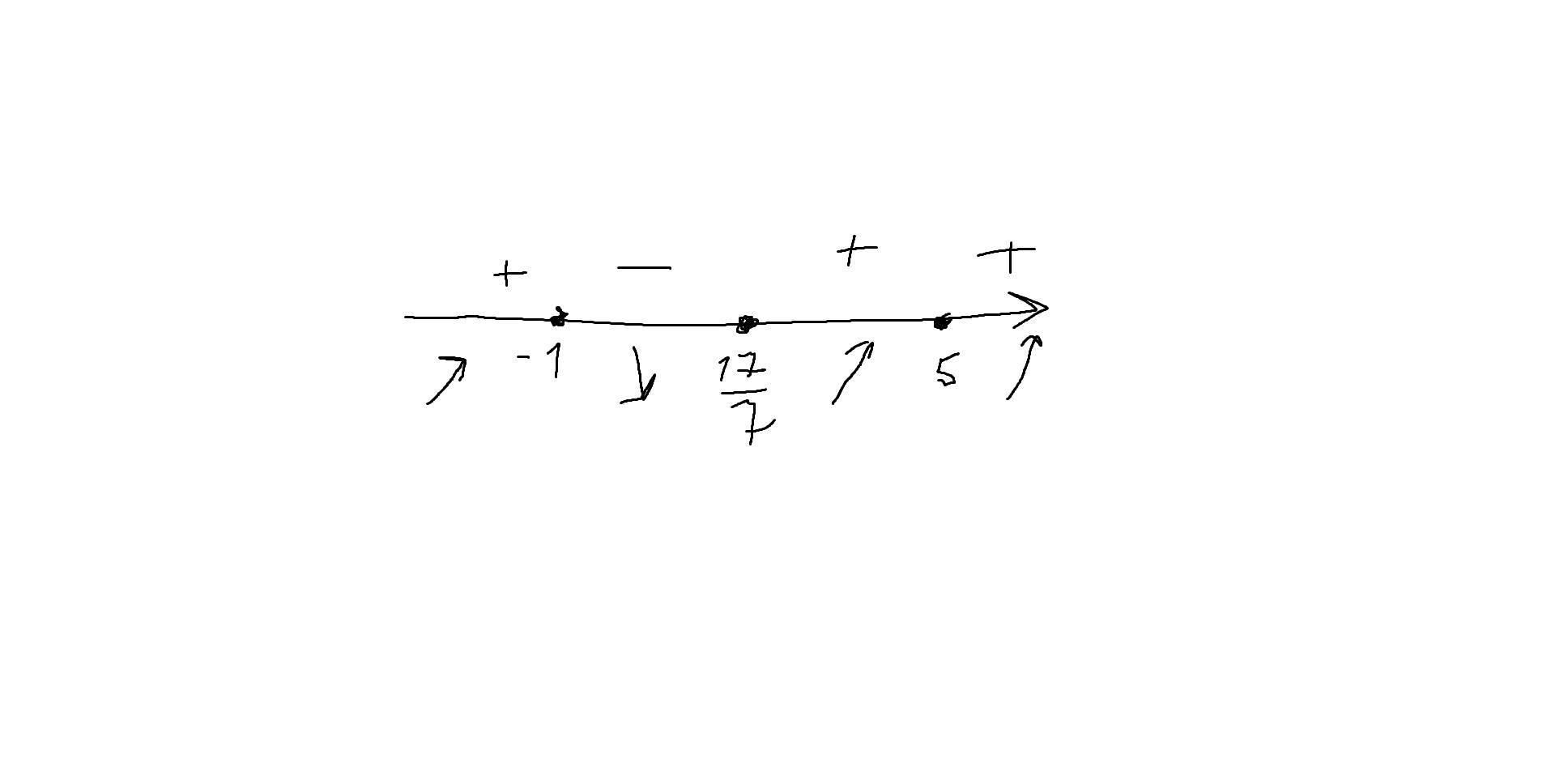
Похожие вопросы
Предмет: Окружающий мир,
автор: Иван213С
Предмет: Русский язык,
автор: shironinavalya
Предмет: Українська мова,
автор: Anka1233
Предмет: Математика,
автор: igorShap
Предмет: Математика,
автор: эдик196