Предмет: Математика,
автор: Ифигения
Найдите производные dy/dx заданных функций
Приложения:
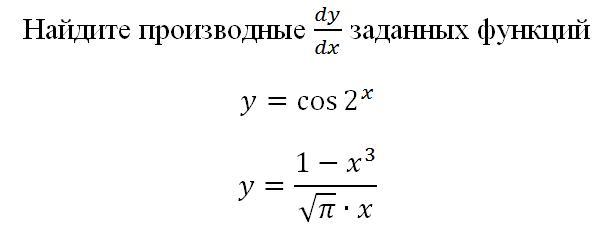
Ответы
Автор ответа:
1
Ответ:
1.
2.
Ифигения:
Большое спасибо!
Похожие вопросы
Предмет: Русский язык,
автор: вппасс
Предмет: Русский язык,
автор: margoamosowa
Предмет: Русский язык,
автор: кокон2
Предмет: Геометрия,
автор: Аноним
Предмет: Математика,
автор: sanfransece