Предмет: Алгебра,
автор: rajhlind
Помогите пожалуйста, решить уравнение
Приложения:
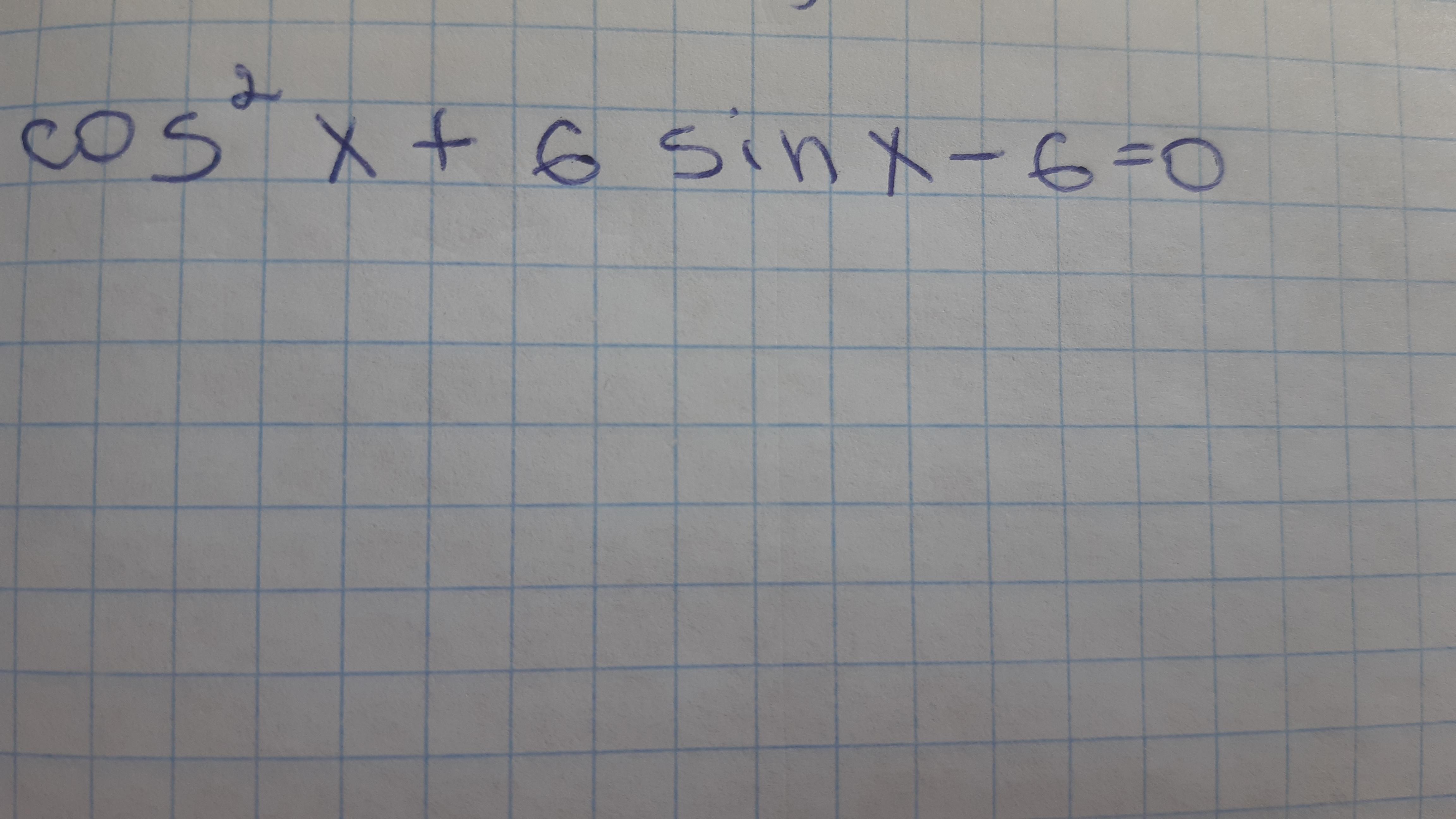
Ответы
Автор ответа:
0
Ответ:
Объяснение:
V означает "или", второе уравнение не имеет корней.
Похожие вопросы
Предмет: Русский язык,
автор: djall12
Предмет: Русский язык,
автор: sobukhoffa
Предмет: Русский язык,
автор: аня1171
Предмет: Алгебра,
автор: джош2
Предмет: Математика,
автор: nurane2