Предмет: Алгебра,
автор: iamsaidovibra
Решите тригонометрическое уравнение
Приложения:
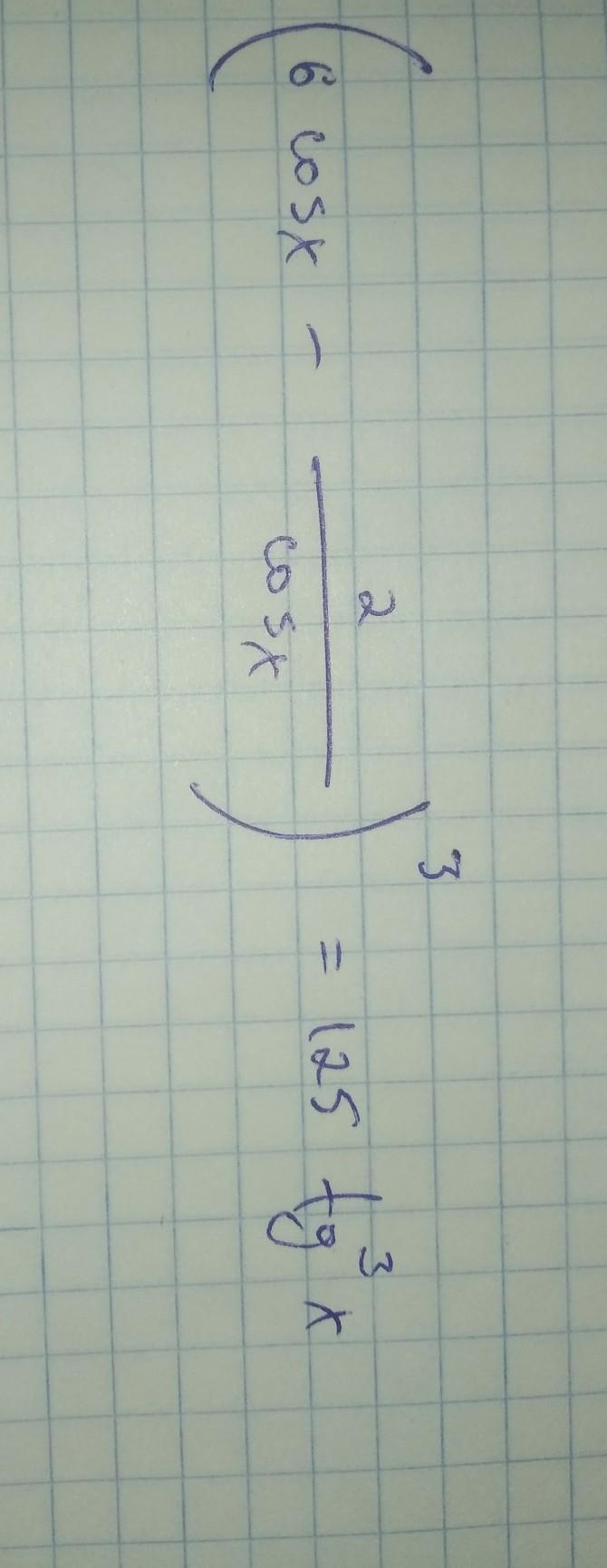
terikovramazan:
(-1)^n*pi/6+2*pi*n, n принадлежит z
Ответы
Автор ответа:
2
Подобным методом решения мы рискуем потерять корни,разве нет?
Вы имеете ввиду,деление на cos x?
Нет.Отбратите внимание на третью строчку.Там избавились от степени путём возведение в кубический корень.
Это имел ввиду
В нечетную степень можно
и потом, она извлекла кубический корень, а не возвела в куб
Понятно.Большое спасибо
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Английский язык,
автор: Danil1234111
Предмет: Английский язык,
автор: Настюшенькааааа
Предмет: Химия,
автор: Ненощька