Предмет: Математика,
автор: vagif404475488
Математический анализ, интегралы
Приложения:
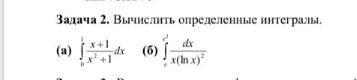
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: vika671
Предмет: Английский язык,
автор: ОпАСнАя2003
Предмет: Русский язык,
автор: английский2
Предмет: Русский язык,
автор: malishplusha
Предмет: Обществознание,
автор: ViBriOn1