Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста!!!
Решите системы уравнений.
Приложения:
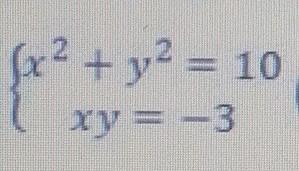
Ответы
Автор ответа:
2
Решим систему методом подстановки.
Выпишем первое уравнение отдельно и решим его.
Решаем биквадратное уравнение:
Теперь найдем х:
Ответ: (-1;3), (1;-3), (-3;1), (3;-1)
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: boykova02
Предмет: Немецкий язык,
автор: nickolaipushki
Предмет: Окружающий мир,
автор: имм4
Предмет: Қазақ тiлi,
автор: alino4kaau
Предмет: Русский язык,
автор: AntonScar100