Методом Мат индукции доказать, что при n принадлежащем к натуральным числам,
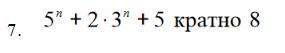
Ответы
Ответ:
Пошаговое объяснение:
1) при n=1
5+2*3+5=16 кратно 8
2) предположим что при n=k
5^k+2*3^k+5 кратно 8 (1)
3) при n=k+1
5^(k+1)+2*3^(k+1)+5=5*5^k+2*3*3^k+5=4*5^k+5^k+2*3^k+4*3^k+5=
=(5^k+2*3^k+5)+4*5^k+4*3^k=(5^k+2*3^k+5)+4*(5^k+3^k)
(5^k+2*3^k+5) кратно 8 по предположению (1)
5^k и 3^k - это нечетные числа так как они являются произведениями нечетных чисел, а сумма двух нечетных чисел четное число ⇒ (5^k+3^k) четное число и оно кратно 2
тогда 4*(5^k+3^k) кратно 8
тогда (5^k+2*3^k+5)+4*(5^k+3^k) кратно 8 как сумма двух чисел кратных 8
из предположения истинности для n=k следует истинность для n=к+1
тогда ⇒ по методу математической индукции
5^n+2*3^n+5 кратно 8 для любого n∈N
При n=1 утверждение верно: 5+6+5=16 делится на 8.
Пусть делится на 8. Тогда
Первая скобка делится на 8 по предположению, а вторая делится на 4 (а после умножения на 10 и на 8). В самом деле, при n=1 скобка равна нулю, а при больших n раскладывается по формуле
Отсюда делаем вывод, что формула методом математической индукции доказана.