Question

3. Отрезок длиной 30 см пересекает плоскость, концы его отстоят от плоскости на 6см и 12 см. Вычислите проекцию этого отрезка на плоскость.

Answer 1

Ответ:

DE = 24 см

Объяснение:

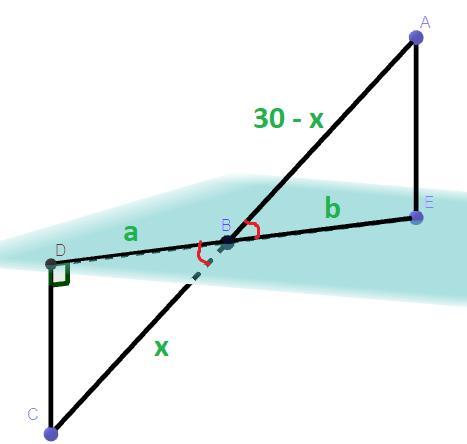
Дано: АС = 30 см, DC = 6 см, AE = 12 см, DC ⊥ ED, AE ⊥ DE

Найти: DE - ?

Решение: Пусть BD = a, BE = b. СB + AB = AC ⇒ AB = AC - BC = 30 - BC.

Пусть BC = x, тогда AB = 30 - x. Треугольник ΔCBD подобен ΔBAE по двум углам так как по условию  DC ⊥ ED, AE ⊥ DE, то ∠CDB = ∠AEB = 90°, а углы ∠DBC = ∠ABE как вертикальные углы, из подобия треугольника ΔCBD треугольнику ΔBAE следует, что

$\left \{ {{\frac{DB}{BE} =\frac{DC}{AE} } \atop {\frac{CB}{BA} =\frac{CD}{AE} }} \right.$ $\left \{ {{DB * AE=BE * DC} \atop {CB * AE=CD * BA}} \right.$ $\left \{ {{12a=6b|:6} \atop {12x=6(30 - x)|:6}} \right.$ $\left \{ {{b=2a} \atop {2x=30 - x}} \right.$$\left \{ {{b=2a} \atop {3x=30|:3}} \right.$ $\left \{ {{b=2a} \atop {x=10}} \right.$

Рассмотрим треугольник ΔCDB. BD = x = 10 см. По теореме Пифагора:

$BD = \sqrt{CB^{2} - CD^{2} } = \sqrt{10^{2} -6^{2} } = \sqrt{100 - 36} = \sqrt{64} = 8$ см.

b = 2a ⇔ BE = 2BD = 2 * 8 = 16 см.

DE = BE + BD = 16 + 8 = 24 см.