Предмет: Алгебра,
автор: Aleesia
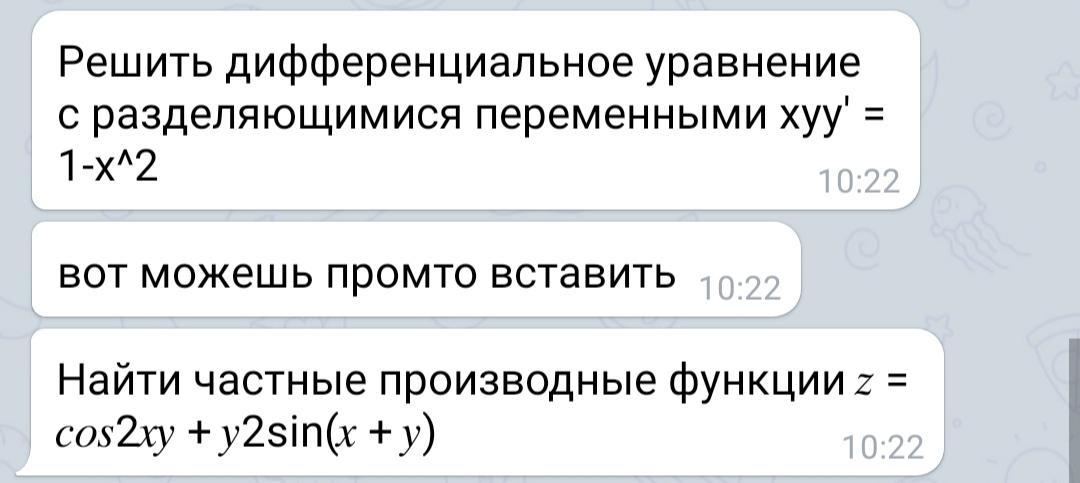
1. Решить дифференциальное уравнение с разделяющимися переменными xyy' = 1-х^2
2. Найти частные производные функции (на фото продолжение)
Приложения:
Ответы
Автор ответа:
1
1.
общее решение
2.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Lanochka11111
Предмет: Химия,
автор: Helpme29382
Предмет: Алгебра,
автор: 1Афина1