Предмет: Математика,
автор: annsu2
Помогите решить. Срочно
Приложения:
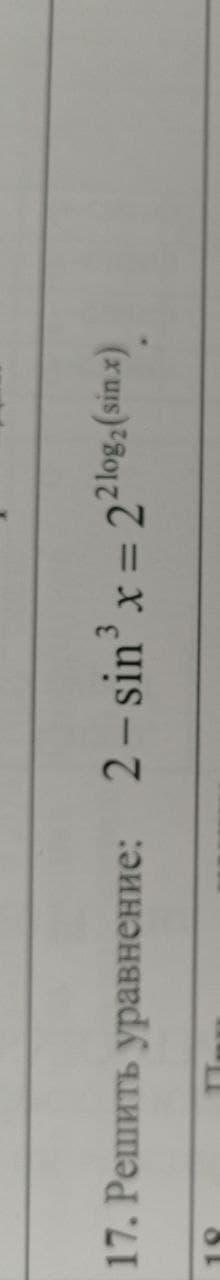
Ответы
Автор ответа:
2
Ответ:
Пошаговое объяснение:
Введём замену:
Перепишем уравнение с учётом замены:
V означает "или", второе уравнение не имеет действительных решений.
Вернёмся к замене:
Похожие вопросы
Предмет: Русский язык,
автор: luntic1
Предмет: Русский язык,
автор: диа38
Предмет: Другие предметы,
автор: ника439
Предмет: Русский язык,
автор: elenashpak200
Предмет: Химия,
автор: КеттиАделин