Предмет: Математика,
автор: sosinittttta
Диференциальные уравнения, высшая математика
Помогите пожалуйста
Приложения:
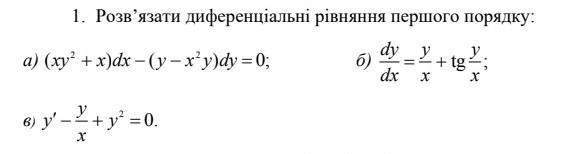
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: натп1
Предмет: Русский язык,
автор: 303099863
Предмет: Окружающий мир,
автор: Аноним
Предмет: Русский язык,
автор: Лизунчик11Няша
Предмет: Физика,
автор: mashaleonteva2