Предмет: Математика, автор: mhlysltnv

срочно!!!!! помогите с интегралами

Приложения:

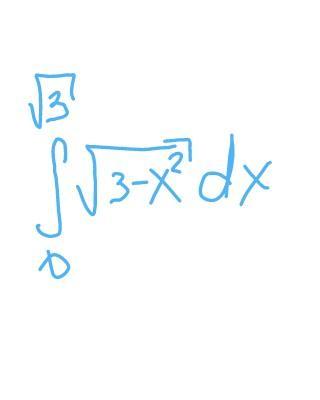
IUV: сделайте замену х = корень(3)*sin(t)

IUV: потом под интегралом получится квадрат косинуса, нужно перейти к косинусу двойного угла, получится сумма двух табличных интегралов

IUV: больше пользы получится если сами попробуете

mhlysltnv: можно это всё в математическом виде? я в математике ноль, а это нужно для учёбы

IUV: печально, хотел чтоб вы попробовали и сами разобрались

mhlysltnv: спасибо, правда. но эта математика мне вообще не даётся сколько не объясняй

mhlysltnv: а высшая тем более

IUV: https://prnt.sc/153gw9o

yugolovin: У Вас в скриншоте ошибка, не приведшая к неправильному ответу - интеграл от косинуса равен синусу, а не минус синусу.

IUV: согласен, с минусом погорячился, но мне повезло - синус нуля и синус пи независимо от знака равны нулю. спасибо )))

Ответы

Автор ответа: yugolovin

1-й способ - используя геометрический смысл определенного интеграла.

Поскольку $y=\sqrt{3-x^2}$ - уравнение верхней половины окружности с центром в начале координат и радиусом $\sqrt{3},$ а пределы интегрирования от нуля до $\sqrt{3},$ интеграл будет равен четверти площади круга радиуса

$\sqrt{3},$ то есть $\frac{\pi(\sqrt{3})^2}{4}=\frac{3\pi}{4}.$

2-й способ. Замена $x=\sqrt3}\sin t; t=\arcsin \frac{x}{\sqrt{3}};\ x=0\Rightarrow t=0;\ x=\sqrt{3}\Rightarrow t=\frac{\pi}{2};\ dx=\sqrt{3}\cos t\,dt;$

$\sqrt{3-x^2}=\sqrt{3}\sqrt{1-\sin^2 t}=\sqrt{3}\sqrt{\cos^2 t}=\sqrt{3}|\cos t|=\sqrt{3}\cos t$

(последнее равенство благодаря тому, что косинус в этом промежутке неотрицателен. Получаем

$\int\limits_0^{\sqrt{3}}\sqrt{3-x^2}\,dx=3\int\limits_0^{\pi/2}\cos^2 t\, dt=\frac{3}{2} \int\limits_0^{\pi/2}(1+\cos 2t)\, dt=\left.\frac{3}{2}(t+\frac{1}{2}\sin 2t)\right|_0^{\pi/2}=$