Предмет: Математика,
автор: bvfuojfdt
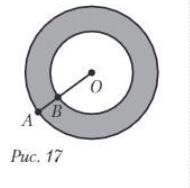
Две окружности расположены так что их центры совпадают.Длина большей окружности на 8Пи см больше длины меньшей окружности.Найдите длину отрезка АВ,если известно что площадь круга,ограниченного большей окружностью,равна 81 пи см2.ПОМОГИТЕ СРОЧНО!ДАЮ 35 БАЛЛОВ
Приложения:
Ответы
Автор ответа:
0
пусть радиус меньшей окружности ; а большей
нам требуется найти AB и мы знаем что AO=AB+BO где AO=
; а
тогда
нам известно площадь меньшей окружности
вычисляется по формуле
нам известно что Длина большей окружности на 8π см больше длины меньшей окружности тогда пусть длина меньшей окружности
а большей
нам известно что
=AB что и требовалось найти Ответ : AB=4cm
Похожие вопросы
Предмет: Английский язык,
автор: ujujuj
Предмет: Русский язык,
автор: guzelka676
Предмет: Русский язык,
автор: 96848b1
Предмет: Геометрия,
автор: AngelSNebesDemonSAda
Предмет: Русский язык,
автор: абк4