Question

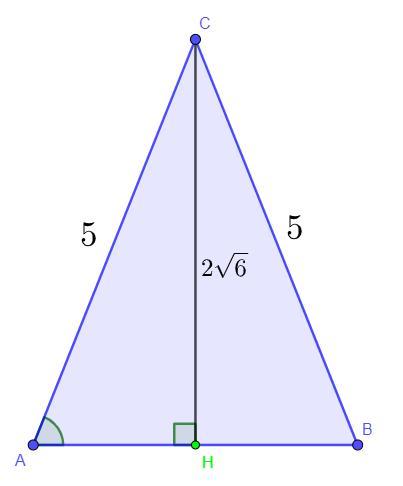
В равнобедренном треугольнике ACB боковые стороны AC и BC равны 5, а высота CH равна 2√6 Найдите косинус угла A. В ответе укажите только число,

Answer 1

Ответ:

Косинус угла А равен 0,2

Объяснение:

Дано: AC = BC = 5, CH = $2\sqrt{6}$, CH - высота ΔABC

Найти: cos ∠A - ?

Решение:

Так как по условию CH - высота ΔABC, то CH ⊥ AB по определению и угол ∠СHA = 90°, следовательно

треугольник ΔCHA - прямоугольный.

Рассмотрим прямоугольный треугольник ΔCHA.

По теореме Пифагора (сумма квадратов катетов равна квадрату гипотенузы):

$AH^{2} + CH^{2} = AC^{2} \Longrightarrow AH =\sqrt{AC^{2} - CH^{2}} =$

$= \sqrt{5^{2} - (2\sqrt{6}) ^{2}} = \sqrt{25 - 24} = \sqrt{1} = 1$.

По определению косинусом угла называют отношение прилежащего к углу катета к гипотенузе, тогда:

$\boldsymbol{ \cos \angle A} = \dfrac{AH}{AC} = \dfrac{1}{5} \boldsymbol{ = 0,2}$.

#SPJ3