Предмет: Алгебра,
автор: berezinaalena303
СРОЧНО ПОМОГИТЕ! ПОЖАЛУЙСТА
Приложения:
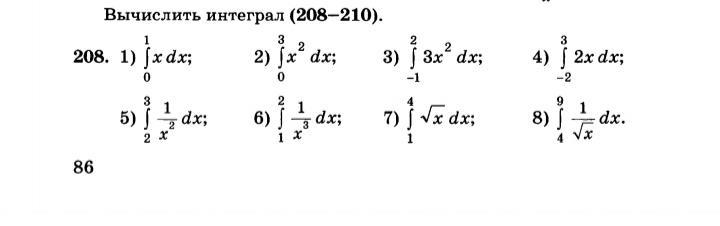
Ответы
Автор ответа:
1
Ответ: На фото
Объяснение: Тут используется первообразные
Приложения:
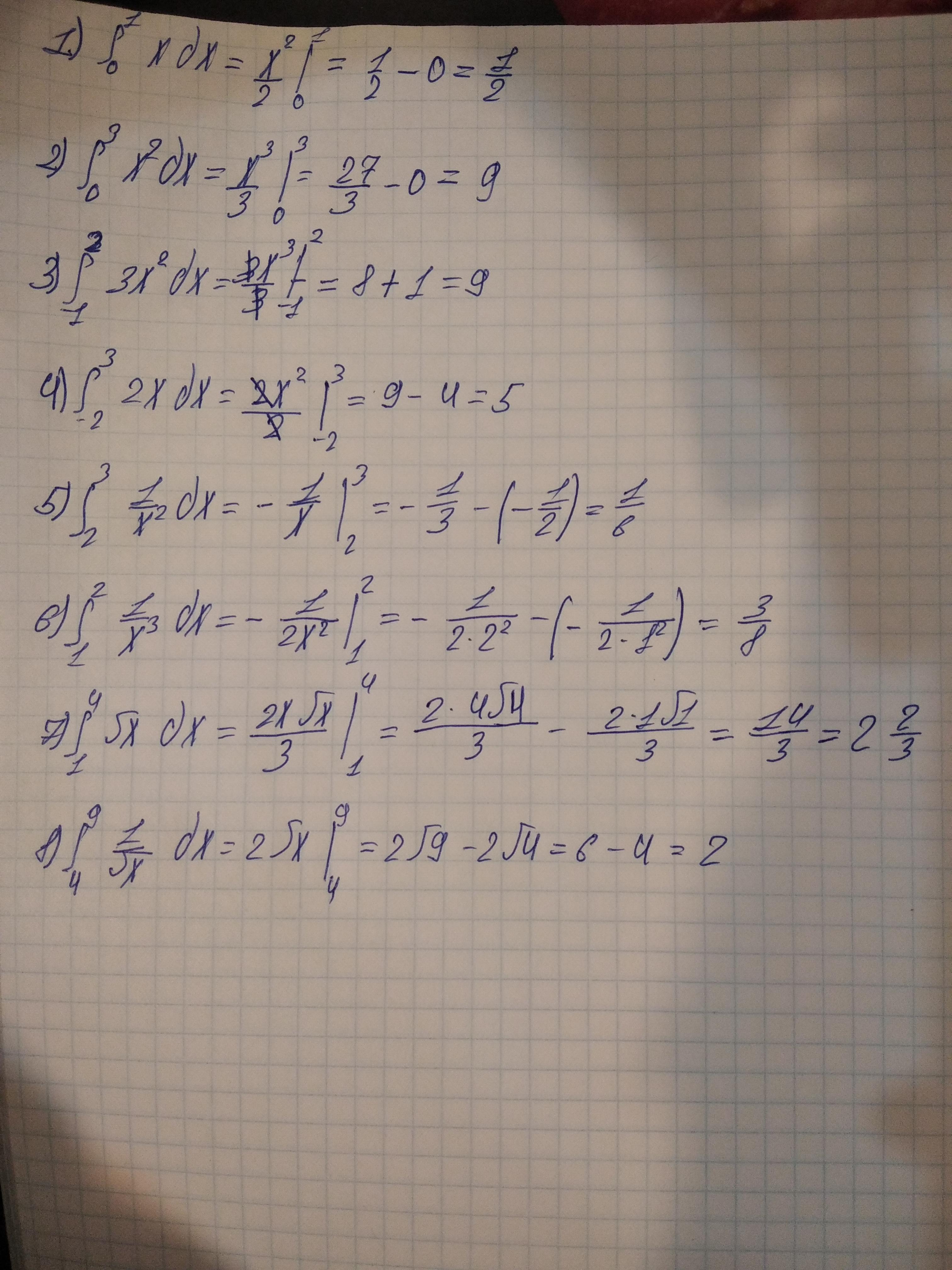
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Русский язык,
автор: давидик2
Предмет: Русский язык,
автор: Тратул
Предмет: Русский язык,
автор: Tilan
Предмет: Алгебра,
автор: zavirohinoleksa