Предмет: Математика,
автор: kekscoopyt
№15 ЕГЭ
Решите пожалуйста
Приложения:
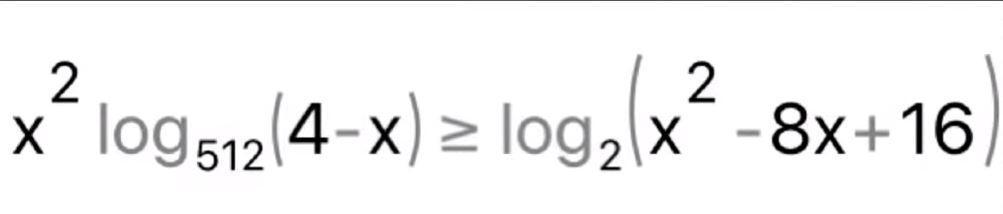
Ответы
Автор ответа:
1
Решение задания прилагаю, исправлено
Приложения:

kekscoopyt:
спасибо
Автор ответа:
0
Ответ:
х∈(-∞; -3√2] ∪[3 ;4)
Пошаговое объяснение:
ОДЗ {4-x>0 , { x<4 ,
{(x-4)²>0 , {x≠4 ⇒ x<4.
Найдем нули
x=√18=3√2 не подходит под одз √18>√16.
, подходит ,тк 3<4.
__+___-3√2__-___3___+___(4)
х∈(-∞; -3√2] ∪[3 ;4)
Похожие вопросы
Предмет: Русский язык,
автор: Qalya5
Предмет: Русский язык,
автор: jtars
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: Diyor11
Предмет: ОБЖ,
автор: veronika25112006