Предмет: Алгебра,
автор: sercy44
Ребята, плиз помогите. Только, напишите по-русски. Откуда, мы взяли эти корни и как решить
Приложения:
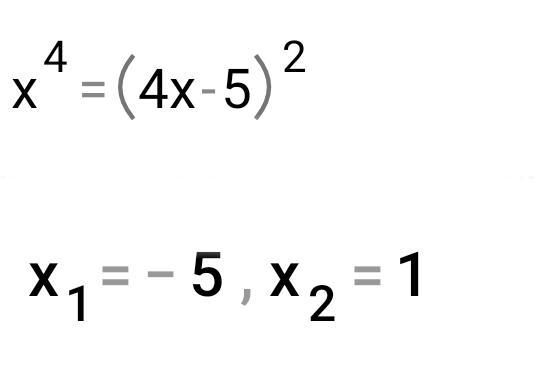
palilov243659:
x^2=4x-5, x^2-4x+5=0, x1=-5 x2=1
И где решение? Оно не решëнное
по теореме Виета
Ответы
Автор ответа:
0
Извлечём квадратнный корень из обоих частей уравнения:
Рассмотрим 3 случая:
Корней нет.
2)
По теореме Виета найдём корни:
Оба корня подходят.
3)
Проверим:
Корень не подходит.
Ответ: -5 , 1
Это всё из Photomath
Я сам решал, и все подробно расписал, чего не ясно?
Похожие вопросы
Предмет: Русский язык,
автор: AVGlazunova123
Предмет: Русский язык,
автор: jijceset
Предмет: Английский язык,
автор: АЛЬБИНА12345678901
Предмет: Русский язык,
автор: элэд
Предмет: Биология,
автор: Катиончик