Предмет: Алгебра,
автор: ksenia123tea
помогите!!!!!!! даю 20 баллов
Приложения:
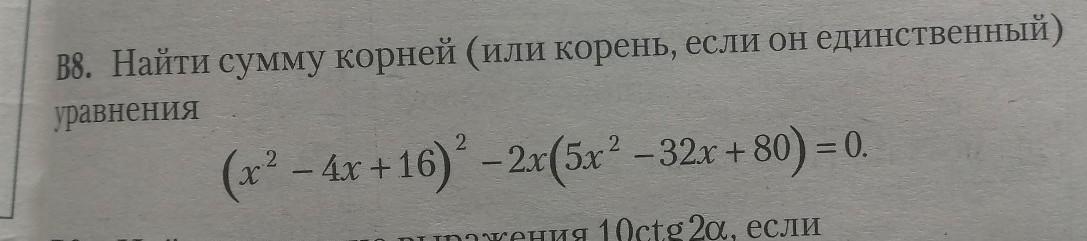
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Попробуем найти корень уравнения подбором:
Одним из корней уравнения является число 2. Разделим многочлен на "x–2":
Попробуем найти корень уравнения подбором:
Разделим многочлен на "x–4":
Решаем уравнение по теореме Виета:
Сложим найденные корни:
Похожие вопросы
Предмет: Английский язык,
автор: ilvira791
Предмет: Русский язык,
автор: enichca87
Предмет: Русский язык,
автор: danil2000smir
Предмет: Математика,
автор: аринаром