Question

Векторы а и b образуют угол 120°, |а|=4, |b|= √3. Найти |2а+b|​

Answer 1

Ответ:

Пошаговое объяснение:

если векторы а и b образуют угол 120°

так как векторы а и 2а сонаправлены то векторы 2а и b также образуют угол 120°

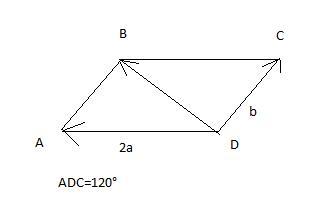
построим векторы 2a и b тогда по правилу  параллелограма суммой векторов 2a и b будет вектор DB

и IDBI=I2a+bI

по свойству параллелограмма угол С=180°-уголD=180°-120°=60°

Рассмотрим треугольник ВСD

BC=I2aI ; CD=IbI

по теореме косинусов

DB²=BC²+CD-2BC*CDcosC=

=4²+(√3)²-2*4*(√3)cos60°=

=16+3-2*4(√3)(1/2)=19-4√3

|2а+b|​=BD=√(19-4√3)