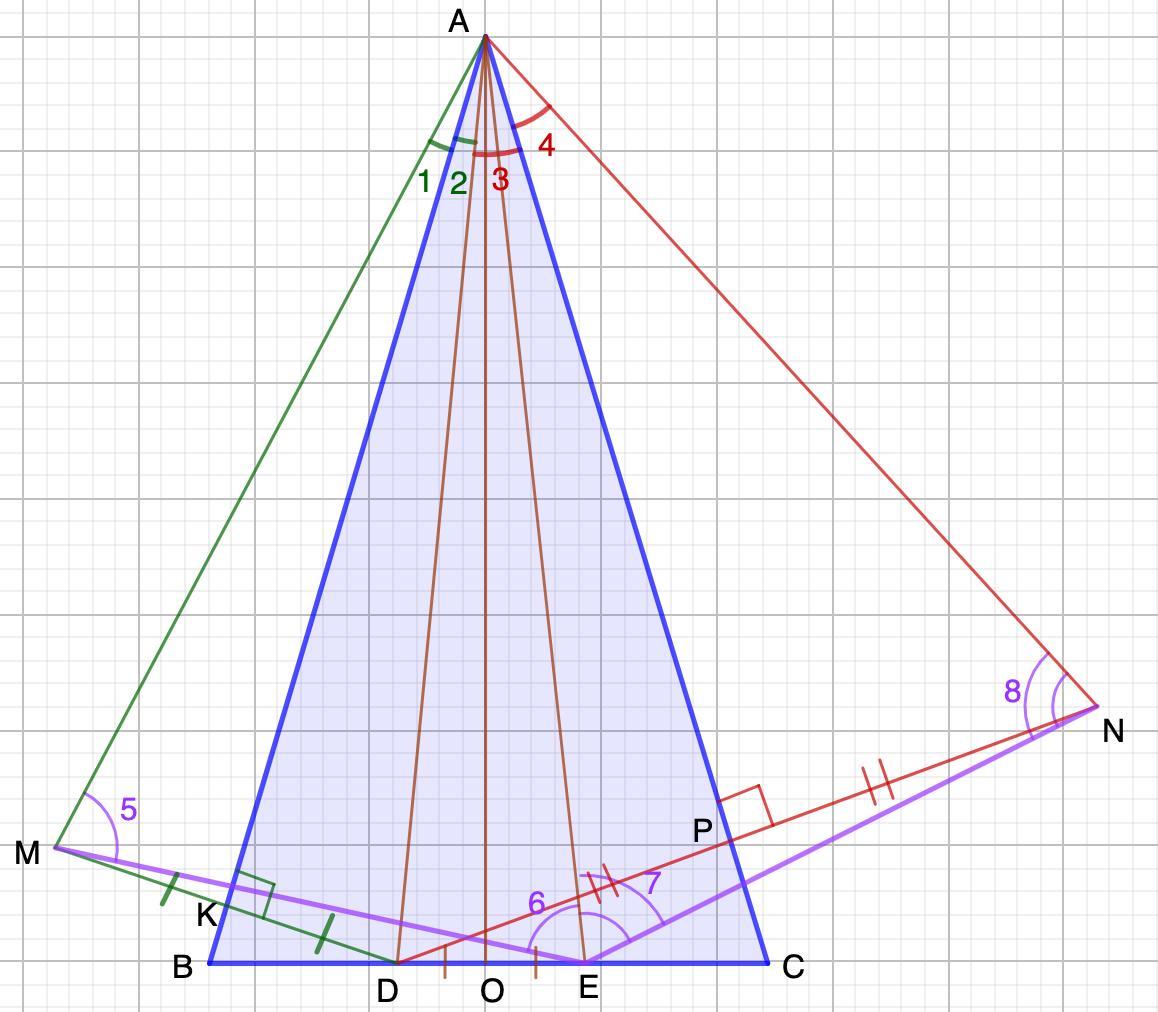
На основании BC равнобедренного треугольника ABC выбрана точка D. Точки M и N симметричны D относительно прямых AB и AC соответственно, точка E симметрична D относительно биссектрисы угла A. Найдите угол MEN, если ∠ABC=68∘.
Ответы
Ответ:
∠MEN=136°
Объяснение:
Точка А симметрична точке В относительно прямой с, если эта прямая делит отрезок АВ пополам и перпендикулярна ему.
Дано: ΔАВС - равнобедренный.
Точки M и N симметричны точке D относительно АВ и АС соответственно.
Точка Е симметрична точке D относительно биссектрисы ∠ВАС.
∠АВС=68°
Найти: ∠MEN
Решение:
1. Рассмотрим ΔMAD.
АК - медиана, высота (условие)
⇒ ΔMAD - равнобедренный ⇒АК - биссектриса.
2. Рассмотрим ΔDAN.
АР - медиана, высота (условие)
⇒ΔDAN - равнобедренный ⇒АР - биссектриса.
3. Рассмотрим ΔАВС - равнобедренный (условие)
⇒∠АВС=∠АСВ=68° (углы при основании)
⇒∠ВАС=180°-(68°+68°)=44° (сумма углов Δ)
4. ∠ВАС=∠2+∠3=44°
⇒∠MAN=∠1+∠2+∠3+∠4=44°·2=88° (п.1 и п.2)
5. Рассмотрим ΔDAE.
АО - медиана, высота (условие)
⇒ΔDAE - равнобедренный ⇒АD=АЕ
6. АМ=АD=АЕ⇒ΔМАЕ - равнобедренный
AN=AD=AE⇒ΔANE - равнобедренный
⇒∠5=∠6; ∠7=∠8.
6. ∠5+∠6+∠7+∠8=360°-88°=272° (сумма углов четырехугольника)
⇒MEN=∠6+∠7=272°:2=136°