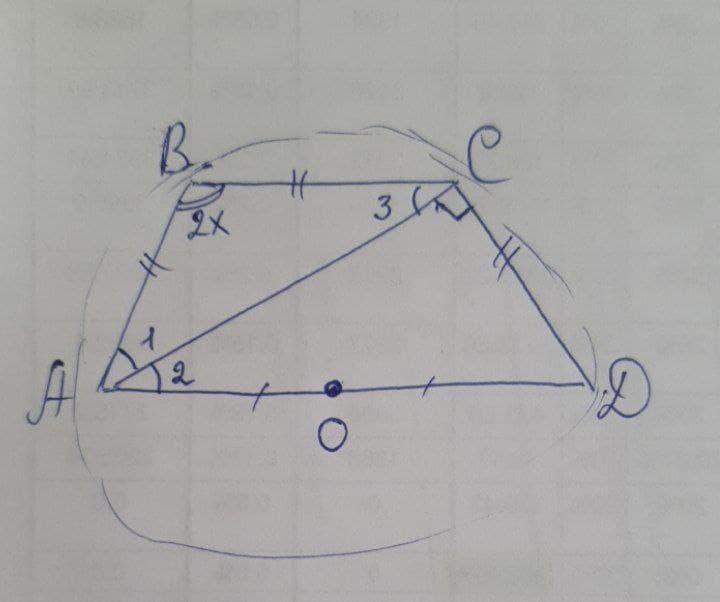
кути трапеції пропорційні числам 1 і 2 , а діагональ є бісектрисою гострого кута. Знайти периметр трапеції , якщо радіус описаного кола дорівнює 8
допоможіть!!!!! пж !!!!! дуже треба!!!!!
Ответы
Ответ:
40см
Объяснение:
Коло можна описати лише навколо рівнобічної трапеції. АВ=СД
∠А:∠В = 1:2
∠А=х, ⇒∠В=2х.
Сума кутів трапеції, прилеглих до бічної сторони, дорівнює 180°:
∠А + ∠В =180
х+2х=180
3х=180
х=60
⇒∠А=60°, ∠В=2х=2*60=120°
Т.к. АС - бісектриса, то ∠1=∠2, Оскількі ВС║АД, то ∠2=∠3 ⇒
ΔАВС - рівнобедрений. АВ=ВС=СД.
За т.косинусів: АС²=АВ²+ВС²-2*АВ*ВС*cos ∠B= 2*АВ²-2*АВ²*cos 120°=
=2*АВ²+АВ²=3*АВ²
ΔАСД: ∠2=60/2=30°, ∠Д=∠А=60° ⇒∠АСД=180-60-30=90°
Прямокутний ΔАСД вписан в коло. Центр кола, описаного навколо прямокутного Δ - середина гіпотенузи АД.
АД - діаметр кола. АД=2*R=2*8=16
т.Піфагора: АД²=АС²+СД² (СД=АВ,)
16²= 3*АВ²+АВ²
4*АВ²=256
АВ²=64
АВ=8 см
АВ=ВС=СД = 8 см, АД=16
Р = АВ+ВС+СД+АД = 3*8+16= 40 см
Ответ:
40 од.
Объяснение:
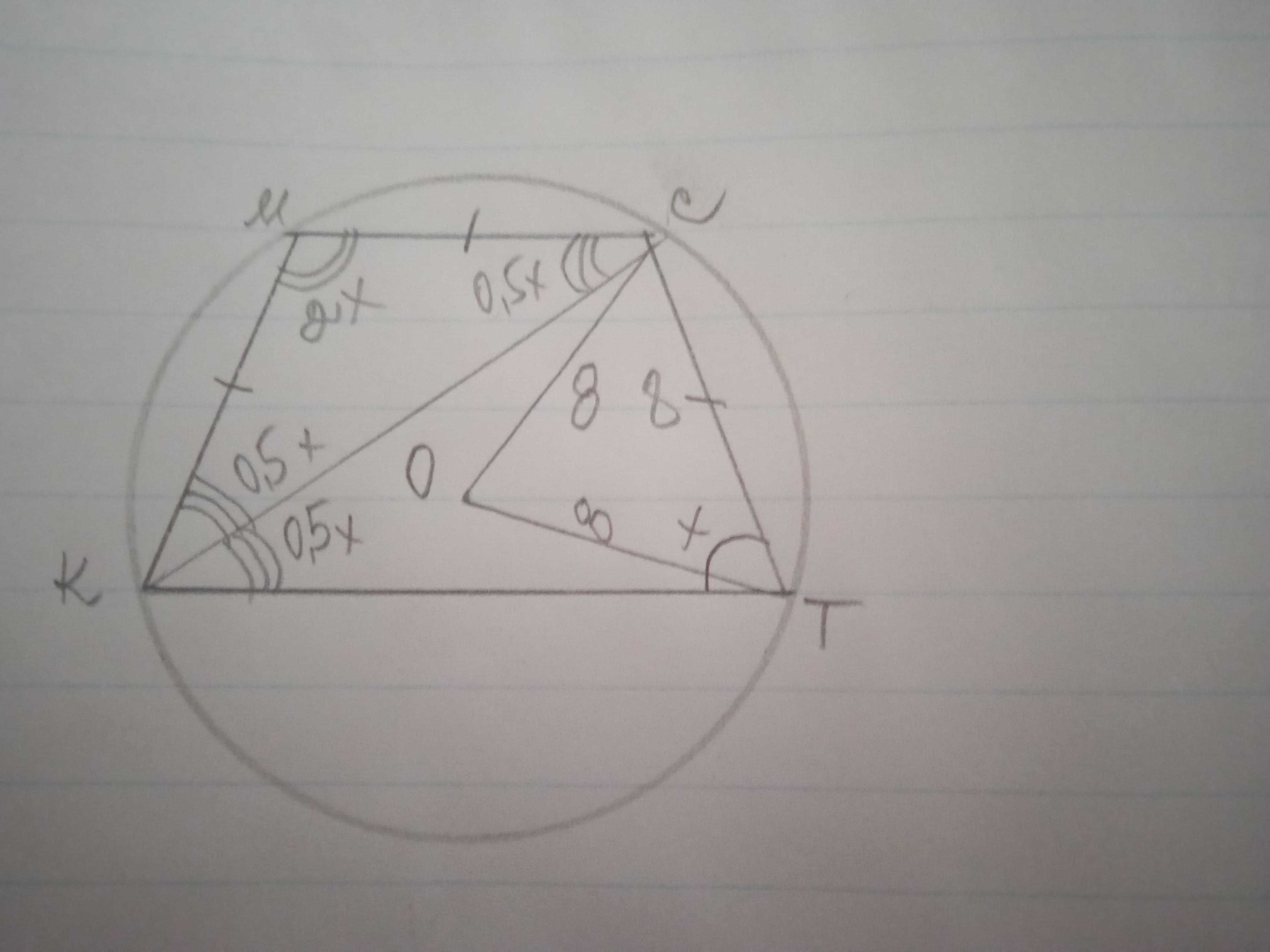
Дано: КМСТ - трапеція, ∠К:∠М=1:2; КС - бісектриса, ∠КМС=∠СКТ; R=8; Знайти периметр Р.
Якщо навколо трапеції можна описати коло, то трапеція є рівнобедреною. Отже КМ=СТ, ∠К=∠С; ∠М=∠Т.
Нехай ∠Т=х°, тоді ∠М=2х°.
∠СКТ=∠МСК як внутрішні при МС║КТ та січній КС.
∠СКТ=∠МСК=∠МКС=0,5х°
Розглянемо ΔКМС - рівнобедрений. КМ=МС.
2х+0,5х+0,5х=180; 3х=180; х=60; ∠М=60*2=120°;
∠МКТ=∠СТК=60°; ∠СКТ=60:2=30°, отже, ΔСКТ - прямокутний.
Розглянемо ΔСОТ - рівнобедрений. ∠СОТ=2∠СКТ за властивістю центрального та вписаного кутів, отже ∠СОТ=60°, тоді ∠ОТС=∠ОСТ=60°, тому що сума кутів трикутника становить 180°.
Отже, ΔОСТ - рівносторонній, СТ=ОС+ОТ=8.
Розглянемо ΔКСТ - прямокутний; СТ=1/2 КТ за властивістю катета, що лежить навпроти кута 30°; КТ=8*2=16.
Знайдемо периметр Р=8+8+8+16=40 од.