Помогите, пожалуйста, с системой
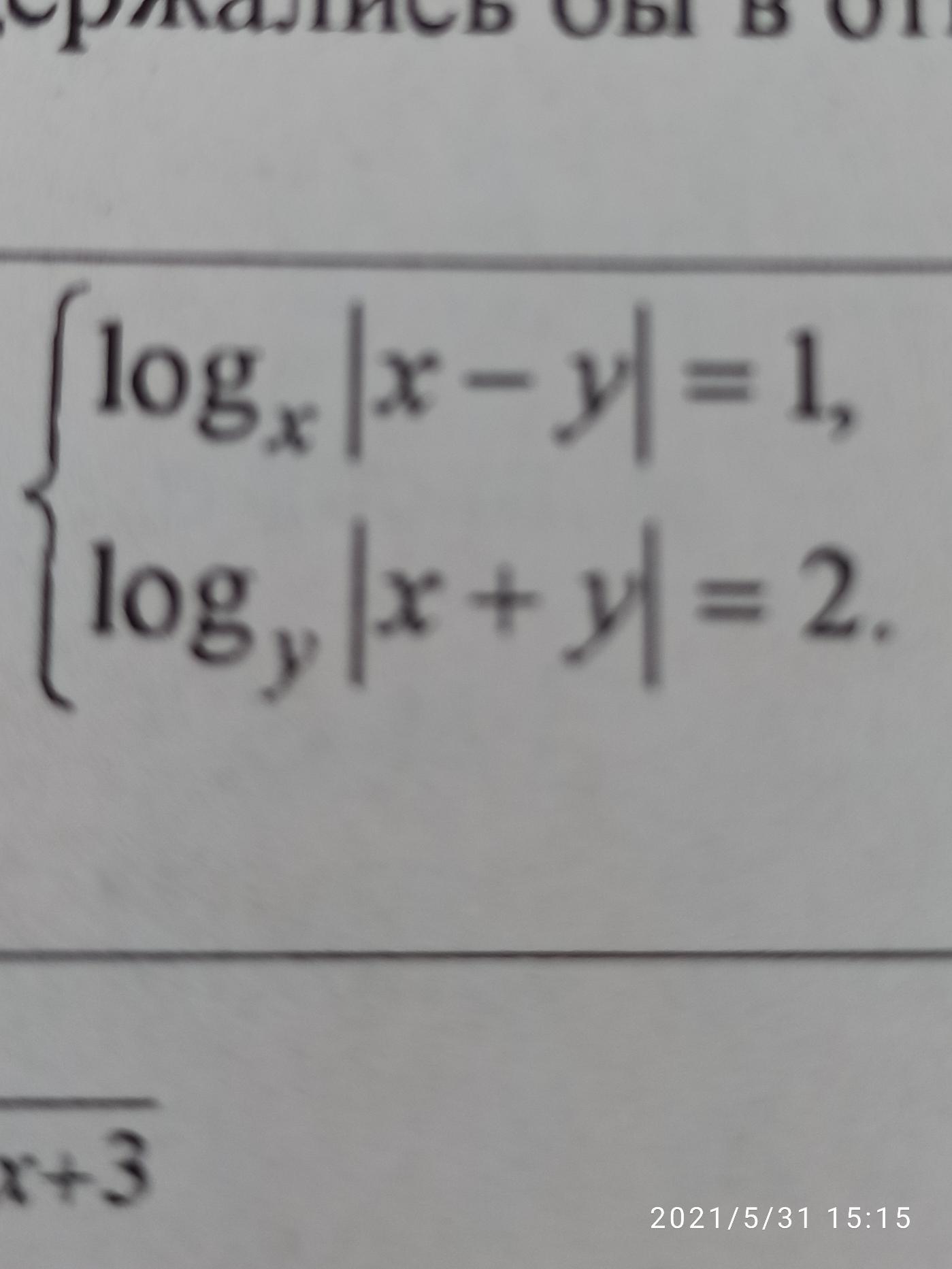
Ответы
Відповідь:
Решеним системы уравнений является
( 3/4, 3/2 )
Пояснення:
log x | x - y | = 1
log y | x + y | = 2
Заменим логарифмические выражения на степенные.
х^1 = | х - у |
у^2 = | х + у |
Наличие модуля накладывает следующие ограничения: в обоих выражениях и левая и правая части не могут принимать отрицательные значения.
х >= 0
у^2 >= 0
х - у >= 0
х + у >=0
Условие про не отрицательность у в квадрате выполняется само ( по определению квадрата числа ), а остальные три ограничения мы обязаны учесть в дальнейшем решении.
При отсутствии модуля уравнения
х = х - у
у^2 = х + у
имеют только нулевые решения.
Из первого уравнения следует, что у = 0.
Подставим у = 0 во второе уравнение и получим, что х = 0.
Наличие модуля дает еще один вариант ответа.
Уравнение
х = | х - у |
имеет не нулевое решение при выполнении следующих условий:
х > 0
у > 0
у = 2х
В этом случае получаем:
х = | х - у | = | х - 2х | = | -х |
Подставим у = 2х в уравнение
у^2 = | х + у |
х = у / 2
у^2 = | х + у | = | у / 2 + у | = | 3у / 2 |
Поскольку система имеет не нулевое решение при выполнении условий:
у > 0
у^2 > 0
то уберем знак модуля.
у^2 = 3/2 × у
Преобразуем уравнение
у × у = 3/2 × у
Отсюда
у = 3/2
х = у/2 = 3/4
Проверка
Подставим
у = 3/2
х = 3/4
в уравнения:
х = | х - у |
у^2 = | х + у |
3/4 = | 3/4 - 3/2 | = | 3/4 - 6/4 | = | -3/4 |
3/4 = | -3/4 |
( 3/2 )^2 = | 3/4 + 3/2 |
Числа под модулем положительные, поэтому модуль убираем.
9/4 = 3/4 + 3/2 = 3/4 + 6/4 = 9/4
9/4 = 9/4
Решеним системы уравнений является
( 3/4, 3/2 )
так как решение ( 0, 0 ) - противоречит области допустимых значений логарифма.
а > 0, в > 0 и а не равно 1. Нулевое решение убираю. Спасибо за подсказку.