кути трапеції пропорційні числам 1 і 2, а діагональ є бісектрисою гострого кута якщо радіус описаного кола дорівнює 8
допоможіть!!!!!!!!!!
Ответы
Ответ: Р = 40
Объяснение:
во вложении

Ответ:
40 од.
Объяснение:
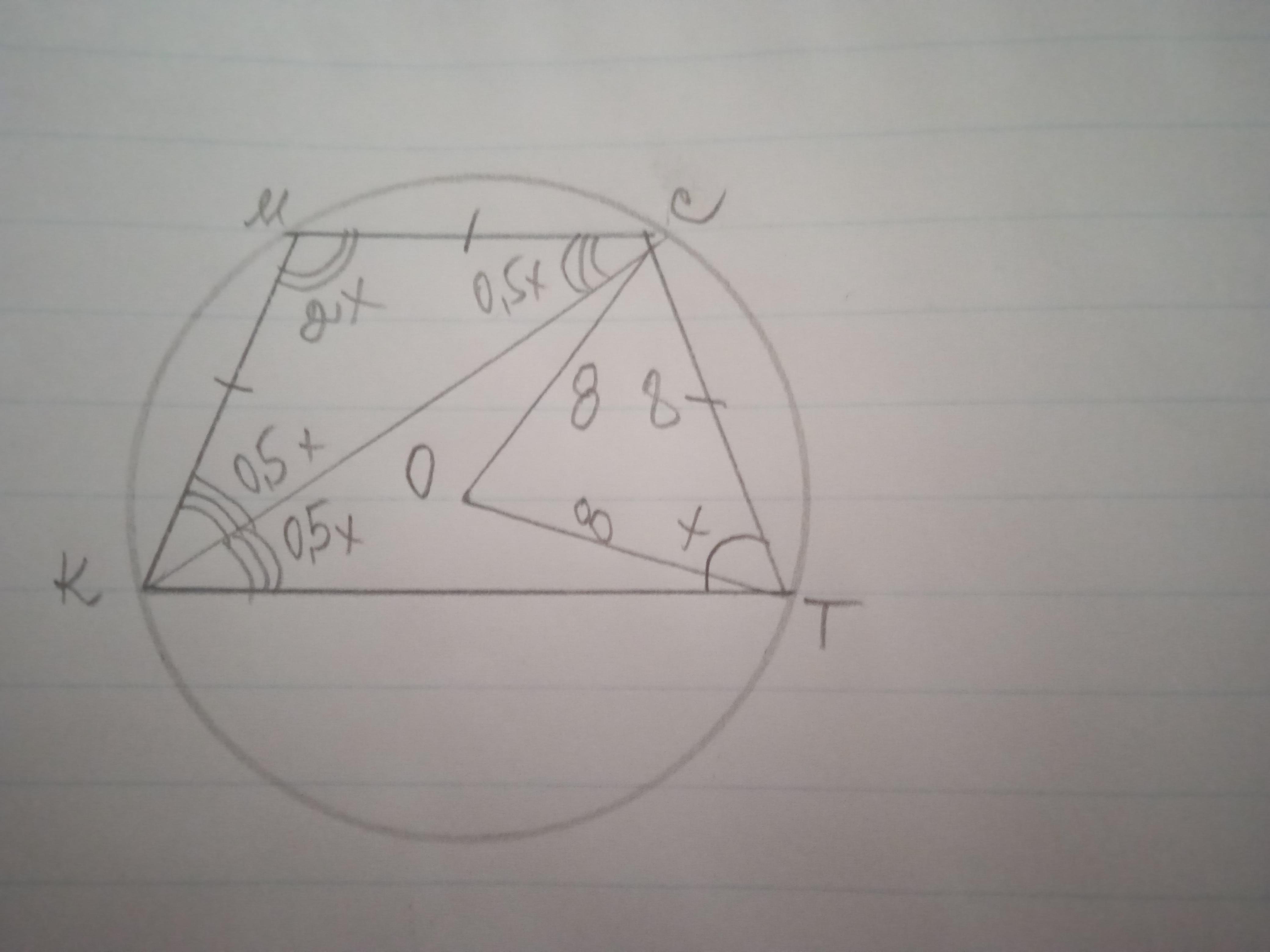
Дано: КМСТ - трапеція, ∠К:∠М=1:2; КС - бісектриса, ∠КМС=∠СКТ; R=8; Знайти периметр Р.
Якщо навколо трапеції можна описати коло, то трапеція є рівнобедреною. Отже КМ=СТ, ∠К=∠С; ∠М=∠Т.
Нехай ∠Т=х°, тоді ∠М=2х°.
∠СКТ=∠МСК як внутрішні при МС║КТ та січній КС.
∠СКТ=∠МСК=∠МКС=0,5х°
Розглянемо ΔКМС - рівнобедрений. КМ=МС.
2х+0,5х+0,5х=180; 3х=180; х=60; ∠М=60*2=120°;
∠МКТ=∠СТК=60°; ∠СКТ=60:2=30°, отже, ΔСКТ - прямокутний.
Розглянемо ΔСОТ - рівнобедрений. ∠СОТ=2∠СКТ за властивістю центрального та вписаного кутів, отже ∠СОТ=60°, тоді ∠ОТС=∠ОСТ=60°, тому що сума кутів трикутника становить 180°.
Отже, ΔОСТ - рівносторонній, СТ=ОС+ОТ=8.
Розглянемо ΔКСТ - прямокутний; СТ=1/2 КТ за властивістю катета, що лежить навпроти кута 30°; КТ=8*2=16.
Знайдемо периметр Р=8+8+8+16=40 од.