Question

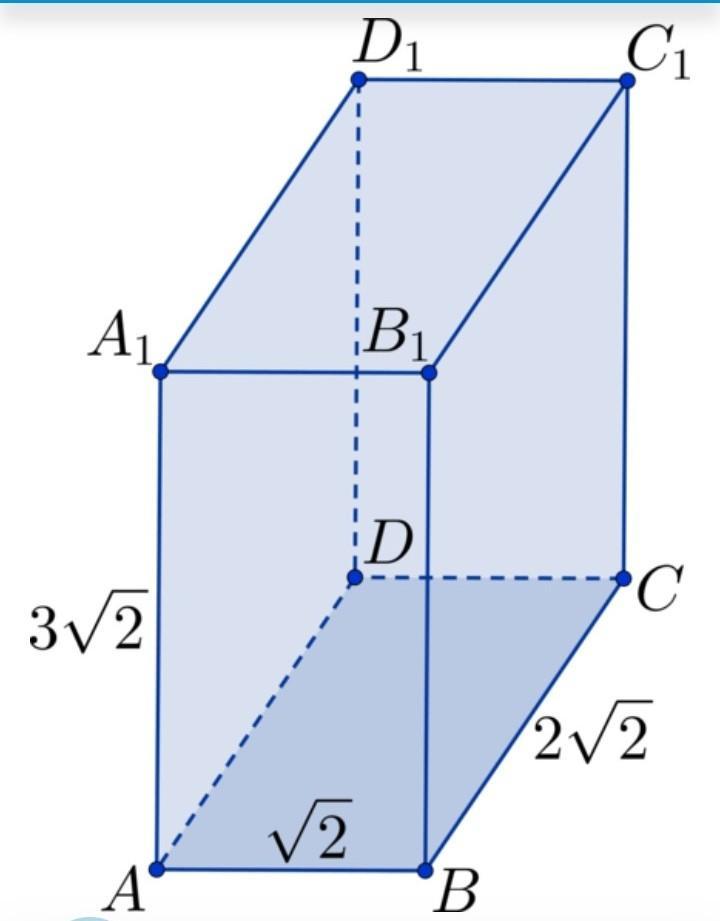
Пожалуйста, умоляю , помогите!: В прямоугольном параллелепипеде ABCDA1B1C1D1: AB=√2, BC=2√2, DD1=3√2. Чему равна длина кратчайшего пути по поверхности параллелепипеда из точки A в точку C1? ​

Answer 1

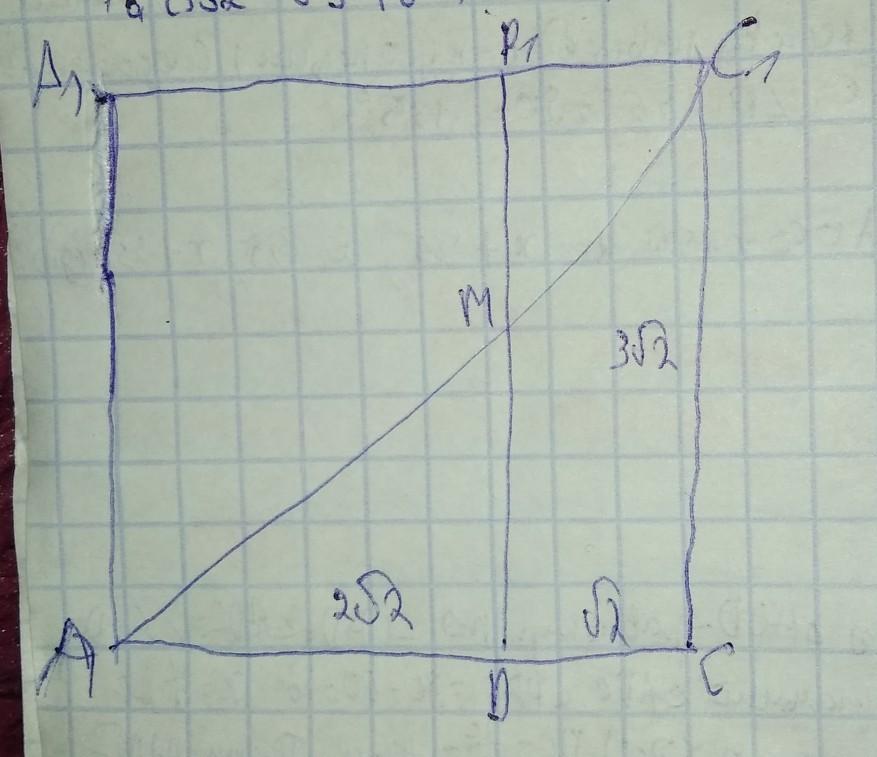
1 Если мы повернем грань DD1C1C вокруг DD1, так чтобы она оказалась в одной плоскости с гранью AA1D1D, а точки C и C1 оказались на продолжении отрезков AD и A1D1 за точки D и D1 соответственно, то получим следующую фигуру:(смотри прикрепленное фото)

2.Очевидно, что кратчайшее расстояние от точки A до точки C1 будет равно длине диагонали AC1. Так как AD+DC=CC1, то AC1 является диагональю квадрата ⇒ AC1=√2⋅3√2=6.

удачи.