Предмет: Геометрия,
автор: Neveroffmark
Радиус вписанной в ромб окружности равен 2, острый угол ромба
равен 30°. Найдите площадь ромба.
Ответы
Автор ответа:
13
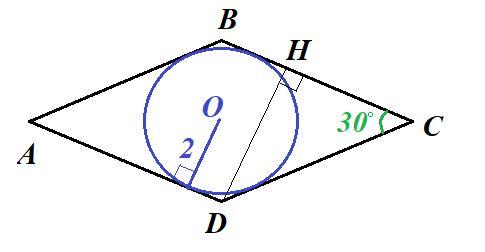
Дано: ромб ABCD, ∠C = 30°,
вписанная окружность с центром О, R = 2.
Найти:
Решение:
Проведём высоту DH ⊥ BC.
Высота ромба равна диаметру вписанной окружности:
DH = 2R = 2·2 = 4
ΔDHC - прямоугольный, ∠DHC=90°, ∠C=30°.
Катет DH, лежащий против угла 30°, равен половине гипотенузы, значит:
DC = 2DH = 2·4 = 8, все стороны ромба равны 8.
Площадь ромба:
Ответ: 32 ед².
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Girl0503
Предмет: Английский язык,
автор: Жанна2611
Предмет: Қазақ тiлi,
автор: test1252
Предмет: Математика,
автор: Ниви
Предмет: ОБЖ,
автор: Аноним