Question

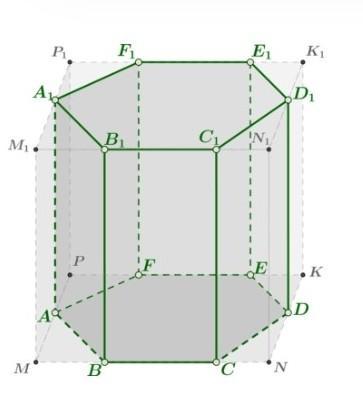
пззз, даю 45!!!: Дана прямая призма, в основании которой лежит правильный шестиугольник ABCDEF. Эту призму вписали в прямоугольный параллелепипед MNKPM1N1K1P1 так, что все вершины обоих оснований призмы лежат на сторонах соответственно обоих оснований параллелепипеда. Причем BC и EF лежат на MN и KP соответственно, а точки A и D – на сторонах MP и NK соответственно. Во сколько раз объем призмы отличается от объема параллелепипеда?​

Answer 1

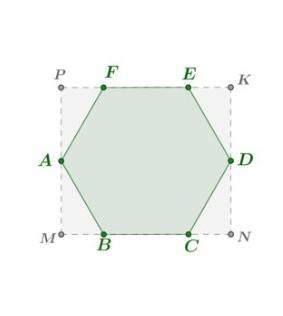
Рассмотрим картинку. Так как параллелепипед прямоугольный, то он прямой и в основании лежит прямоугольник. Следовательно, его боковые ребра (например, MM1) параллельны боковым ребрам призмы и равны, так как основания призмы вписаны в основания параллелепипеда (то есть лежат в одних и тех же плоскостях). Отсюда следует, что высоты призмы и параллелепипеда одинаковы. Пусть h – длина их высоты. Рассмотрим отдельно основание. По свойству правильного шестиугольника BF⊥FE. Так как MNKP – прямоугольник, то есть MP⊥PK, то MP∥BF. Заметим также, что вообще говоря MP=BF, а PK=AD. Пусть a – сторона шестиугольника. Его угол равен 120∘, следовательно, по теореме косинусов:

$BF {}^{2} =a {}^{2} +a {}^{2} −2a⋅a⋅cos⁡120∘=3a {}^{2} ⇒MP=a \sqrt{} {} 3.$

Заметим также, что ∠MAB=30∘, следовательно, в треугольнике MAB : sin⁡30∘=MB/AB⇒MB=1/2a.

Следовательно, MN=1/2a+a+1/2a=2a. Значит, MNKP – прямоугольник со сторонами a√3 и 2a. Площадь правильного шестиугольника равна 3√3/2a², следовательно, объем призмы :

$Vprism= \frac{3 \sqrt{3} }{2} a {}^{2} h$

а объем параллелепипеда:

$Vparallel=a \sqrt{} {3}^{2} ⋅2a⋅h=2 \sqrt{} 3a {}^{2} h$

следовательно ,

$\frac{vprizm}{Vparallel} = \frac{3}{4} =0,75.</p><p></p><p>$

объяснение

Одна из самых долгих моих задач, может получит значок *поверенный*...