решите уравнение! пожалуйста!!!!!
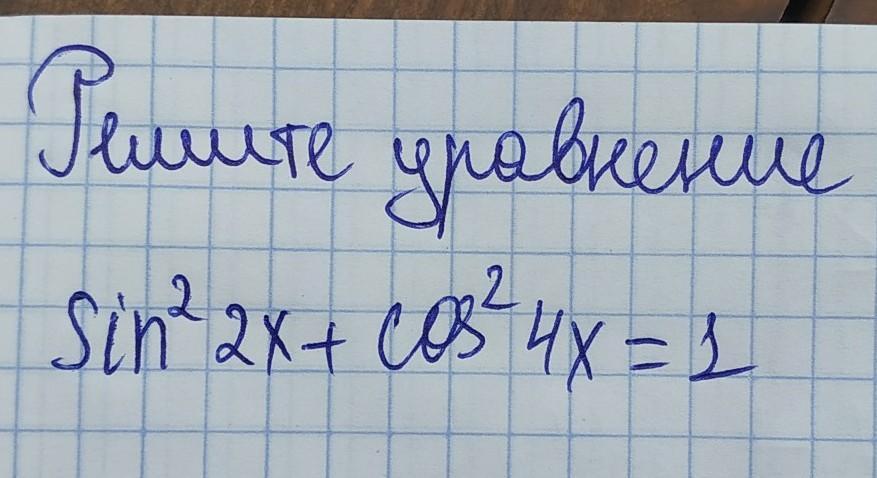
Ответы
sin^2(2x)+cos^2(4x)=sin^2(2x)+cos^2(2x)
cos^2(4x)-cos^2(2x)=0
(cos(4x)-cos(2x))(cos(4x)+cos(2x))=0-оба множителя могут быть 0
1)cos(4x)-cos(2x)=0;
-2sin(3x)*sinx=0; sin3x=0; 3x=pik; x1=pik/3
sinx=0; x2=pin
2)cos(4x)+cos(2x)=0
2cos(3x)cosx=0; cos(3x)=0;3x=pi/2+pim; x3=pi/6+pim/3
cos x=0; x4=pi/2+pil
k;n;m;l-целые
Ответ:
,
где k∈Z.
Пошаговое объяснение:
Запишем наше уравнение:
Квадрат синуса любого угла можно представить в виде:
То есть, наш мы можем представить в виде:
(1)
Квадрат косинуса любого угла можно представить в виде:
Тогда наш мы можем представить в виде:
(2)
Теперь подставим полученные значения (1) и (2) в начальное наше уравнение:
Избавляемся от знаменателя, домножив единицу на 2:
Раскроем скобки, а затем оставим в левой части значения косинусов, а в правую перебросим целые числа, получим:
Теперь вспомним формулу разности косинусов двух разных углов, которая имеет вид:
(3)
Преобразуем по формуле (3) наши косинусы:
Теперь мы имеем право разделить наше уравнение на два равных нулю:
и
Разберём уравнение :
Это "особый случай" решения синуса (их три: при , тоже самое и для косинуса). В данном случае корень уравнения будет иметь вид:
,где k∈Z.
Теперь разберём второе уравнение: :
,где k∈Z.
Получаем ответ:
,где k∈Z.